Acerca de la fórmula de Euler

En el ámbito de los números complejos, al integrar expresiones trigonométricas, es probable que encontremos la denominada fórmula de Euler.

Nombrada en honor al legendario matemático Leonhard Euler, esta poderosa ecuación merece un examen más detallado — con el fin de que podamos utilizarla en todo su potencial.

Examinaremos cómo la fórmula de Euler nos permite expresar números complejos como exponenciales, y exploraremos las diferentes formas en que puede establecerse con relativa facilidad.

Además, consideraremos también sus diversas aplicaciones, tales como el caso particular de la identidad de Euler, la forma exponencial de los números complejos, definiciones alternativas de funciones clave y demostraciones alternativas del teorema de De Moivre y las identidades trigonométricas aditivas.

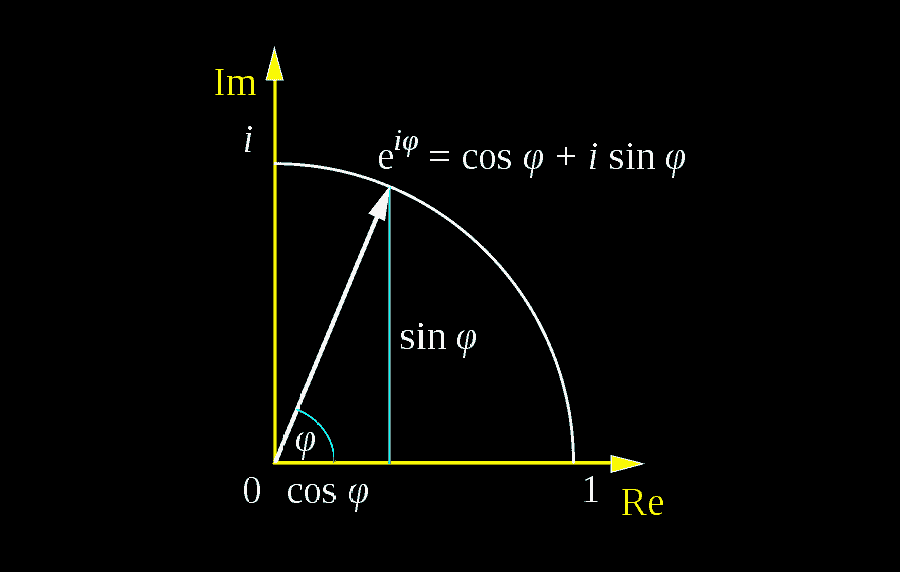
La Fórmula de Euler Explicada: Introducción, Interpretación y Ejemplos

Entonces, ¿qué es exactamente la fórmula de Euler? En resumen, es el teorema que establece que

eix=cos⁡x+isin⁡x

donde:

• x es un número real.
• e es la base del logaritmo natural.
• i es la unidad imaginaria (es decir, la raíz cuadrada de −1).

La fórmula de Euler establece la relación fundamental entre las funciones trigonométricas y las funciones exponenciales. Geométricamente, puede considerarse como una forma de unir dos representaciones del mismo número complejo unitario en el plano complejo.

Examinemos algunos de los valores clave de la fórmula de Euler, y veamos cómo se corresponden con puntos en el círculo trigonométrico/unitario:

• Para x=0, tenemos e0=cos⁡0+isin⁡0, lo que da como resultado 1=1. Hasta ahora, todo bien: sabemos que un ángulo de 0 en el círculo trigonométrico es 1 en el eje real, y esto es lo que obtenemos aquí.
• Para x=1, tenemos ei=cos⁡1+isin⁡1. Este resultado sugiere que ei es precisamente el punto en el círculo unitario cuyo ángulo es 1 radián.
• Para x=π2, tenemos eiπ2=cos⁡π2+isin⁡π2=i. Este resultado es útil en algunos cálculos relacionados con la física.
• Para x=π, tenemos eiπ=cos⁡π+isin⁡π, lo que significa que eiπ=−1. Este resultado es equivalente a la famosa identidad de Euler.
• Para x=2π, tenemos ei(2π)=cos⁡2π+isin⁡2π, lo que significa que ei(2π)=1, igual que con x=0.

Una clave para comprender la fórmula de Euler radica en reescribir la fórmula de la siguiente manera:(ei)x=cos⁡x+isin⁡xdonde:

• La expresión de la derecha puede considerarse como el número complejo unitario con ángulo x.
• La expresión de la izquierda puede considerarse como el número complejo unitario de 1 radián elevado a x.

Y dado que elevar un número complejo unitario a una potencia puede considerarse como multiplicaciones repetidas (es decir, sumar ángulos en este caso), la fórmula de Euler puede interpretarse como dos formas diferentes de recorrer el círculo unitario para llegar al mismo punto.

Derivaciones

La fórmula de Euler puede establecerse al menos de tres maneras. La primera derivación se basa en series de potencias, donde las funciones exponencial, seno y coseno se expanden como series de potencias para concluir que la fórmula efectivamente se cumple.

La segunda derivación de la fórmula de Euler se basa en el cálculo, en el que ambos lados de la ecuación se tratan como funciones y se diferencian en consecuencia. Esto conduce a la identificación de una propiedad común, que puede ser explotada para demostrar que ambas funciones son efectivamente iguales.

Otra derivación más de la fórmula de Euler implica el uso de coordenadas polares en el plano complejo, a través de las cuales se encuentran posteriormente los valores de r y θ. De hecho, es posible que usted pueda adivinar cuáles son estos valores, ¡simplemente observando la fórmula en sí!

Derivación 1: Series de Potencias

Una de las derivaciones más intuitivas de la fórmula de Euler implica el uso de series de potencias. Consiste en expandir las series de potencias de la exponencial, el seno y el coseno, para finalmente concluir que la igualdad se cumple.

Como advertencia, este enfoque asume que las expansiones en series de potencias de sin⁡z, cos⁡z, y ez son absolutamente convergentes en todas partes (es decir, que se cumplen para todos los números complejos z). Sin embargo, también tiene la ventaja de demostrar que la fórmula de Euler se cumple para todos los números complejos z también.

Para una variable compleja z, la expansión en serie de potencias de ez es ez=1+z1!+z22!+z33!+z44!+⋯ Ahora, tomemos z como ix (donde x es un número complejo arbitrario). A medida que z se eleva a potencias crecientes, i también se eleva a potencias crecientes. Las primeras ocho potencias de i se ven así: (por la definición de ) i0=1 i4=i2⋅i2=1 i1=i i5=i⋅i4=i i2=−1 (por la definición de i) i6=i⋅i5=−1 i3=i⋅i2=−i i7=i⋅i6=−i (observe la ciclicidad de las potencias de i: 1, i, −1, −i. Utilizaremos estas potencias en breve.)

Con z=ix, la expansión de ez se convierte en: eix=1+ix+(ix)22!+(ix)33!+(ix)44!+⋯ Extrayendo las potencias de i, obtenemos: eix=1+ix−x22!−ix33!+x44!+ix55!−x66!−ix77!+x88!+⋯ Y dado que la expansión en serie de potencias de ez es absolutamente convergente, podemos reorganizar sus términos sin alterar su valor. Agrupando los términos reales y términos imaginarios juntos, obtenemos: eix=(1−x22!+x44!−x66!+x88!−⋯)+i(x−x33!+x55!−x77!+⋯) Ahora, hagamos un desvío y veamos las series de potencias del seno y coseno. La serie de potencias de cos⁡x es cos⁡x=1−x22!+x44!−x66!+x88!−⋯ Y para sin⁡x, es sin⁡x=x−x33!+x55!−x77!+⋯ En otras palabras, la última ecuación que teníamos es precisamente eix=cos⁡x+isin⁡x que es la declaración de la fórmula de Euler que estábamos buscando.

Derivación 2: Cálculo

Otra forma elegante de establecer la fórmula de Euler es considerar tanto eix como cos⁡x+isin⁡x como funciones de x, antes de diferenciarlas para encontrar alguna propiedad común entre ellas.

Para que eso suceda, sin embargo, uno debe asumir que las funciones ez, cos⁡x y sin⁡x están definidas y son diferenciables para todos los números reales x y números complejos z. Al asumir que estas funciones son diferenciables para todos los números complejos, también es posible demostrar que la fórmula de Euler se cumple para todos los números complejos.

En primer lugar, sean f1(x) y f2(x) eix y cos⁡x+isin⁡x, respectivamente. Diferenciando f1 mediante la regla de la cadena se obtiene:f1′(x)=ieix=if1(x)De manera similar, diferenciando f2 también se obtiene:f2′(x)=−sin⁡x+icos⁡x=if2(x)En otras palabras, ambas funciones satisfacen la ecuación diferencial f′(x)=if(x). Ahora, considérese la función f1f2, que está bien definida para todo x (dado que f2(x)=cos⁡x+isin⁡x corresponde a puntos en el círculo unitario, que nunca son cero). Establecido esto, utilizando la regla del cociente en esta función se obtiene:(f1f2)′(x)=f1′(x)f2(x)−f1(x)f2′(x)[f2(x)]2=if1(x)f2(x)−f1(x)if2(x)[f2(x)]2=0Y dado que la derivada aquí es 0, esto implica que la función f1f2 debe haber sido una constante desde el principio. ¿Cuál es el valor de esta constante? Averigüémoslo sustituyendo x=0 en la función:(f1f2)(0)=ei0cos⁡0+isin⁡0=1En otras palabras, debemos tener que para todo x:(f1f2)(x)=eixcos⁡x+isin⁡x=1que, después de mover cos⁡x+isin⁡x a la derecha, se convierte en la famosa fórmula que hemos estado buscando.

Derivación 3: Coordenadas Polares

Otra ingeniosa demostración de la fórmula de Euler implica tratar los exponenciales como números, o más específicamente, como números complejos en coordenadas polares.

En efecto, ya sabemos que todos los números complejos no nulos pueden expresarse en coordenadas polares de manera única. En particular, cualquier número de la forma eix (con x real), que es no nulo, puede expresarse como:eix=r(cos⁡θ+isin⁡θ)donde θ es su ángulo principal desde el eje real positivo (con, digamos, 0≤θ<2π), y r es su radio (con r>0). No hacemos ninguna suposición sobre los valores de r y θ, excepto el hecho de que son funciones de x (que pueden o no contener x como variable). Serán determinados en el curso de la demostración.

(Sin embargo, lo que sí sabemos es que cuando x=0, el lado izquierdo es 1, lo que implica que r y θ satisfacen las condiciones iniciales de r(0)=1 y θ(0)=0, respectivamente.)

A efectos prácticos, comenzaremos diferenciando ambos lados de la ecuación. Por la definición de exponencial, diferenciar el lado izquierdo de la ecuación con respecto a x produce ieix. Después de diferenciar el lado derecho de la ecuación, la ecuación se convierte en:ieix=drdx(cos⁡θ+isin⁡θ)+r(−sin⁡θ+icos⁡θ)dθdxEstamos buscando una expresión que esté únicamente en términos de r y θ. Para deshacernos de eix, sustituimos r(cos⁡θ+isin⁡θ) por eix para obtener:ir(cos⁡θ+isin⁡θ)=(cos⁡θ+isin⁡θ)drdx+r(−sin⁡θ+icos⁡θ)dθdxUna vez ahí, distribuyendo la i en el lado izquierdo se obtiene:r(icos⁡θ−sin⁡θ)=(cos⁡θ+isin⁡θ)drdx+r(−sin⁡θ+icos⁡θ)dθdxIgualando las partes imaginarias y partes reales, respectivamente, obtenemos:ircos⁡θ=isin⁡θdrdx+ircos⁡θdθdxy−rsin⁡θ=cos⁡θdrdx−rsin⁡θdθdxLo que tenemos aquí es un sistema de dos ecuaciones y dos incógnitas, donde dr/dx y dθ/dx son las variables. Podemos resolverlo en unos pocos pasos. Primero, asignando α a dr/dx y β a dθ/dx, obtenemos:(I)(II)(I)rcos⁡θ=(sin⁡θ)α+(rcos⁡θ)β(II)−rsin⁡θ=(cos⁡θ)α−(rsin⁡θ)βSegundo, multiplicando (I) por cos⁡θ y (II) por sin⁡θ, obtenemos:(III)(IV)(III)rcos2⁡θ=(sin⁡θcos⁡θ)α+(rcos2⁡θ)β(IV)−rsin2⁡θ=(sin⁡θcos⁡θ)α−(rsin2⁡θ)βEl propósito de estas operaciones es eliminar α haciendo (III) – (IV), y cuando lo hacemos, obtenemos:r(cos2⁡θ+sin2⁡θ)=r(cos2⁡θ+sin2⁡θ)βDado que cos2⁡θ+sin2⁡θ=1, emerge una ecuación más simple:r=rβY dado que r>0 para todo x, esto implica que β — que habíamos establecido como dθ/dx — es igual a 1.

Una vez ahí, sustituyendo este resultado de vuelta en (I) y (II) y haciendo algunas cancelaciones, obtenemos:0=(sin⁡θ)α0=(cos⁡θ)αlo que implica que α — que habíamos establecido como drdx — debe ser igual a 0.

Del hecho de que dr/dx=0, podemos deducir que r debe ser una constante. Similarmente, del hecho de que dθ/dx=1, podemos deducir que θ=x+C para alguna constante C.

Sin embargo, dado que r satisface la condición inicial r(0)=1, debemos tener que r=1. Similarmente, porque θ satisface la condición inicial θ(0)=0, debemos tener que C=0. Es decir, θ=x.

Con r y θ ahora identificados, podemos entonces sustituirlos en la ecuación original y obtener:eix=r(cos⁡θ+isin⁡θ)=cos⁡x+isin⁡xque, como se esperaba, es exactamente el enunciado de la fórmula de Euler para números reales x.

Aplicaciones

Siendo una de las ecuaciones más importantes en matemáticas, la fórmula de Euler ciertamente tiene su justa proporción de interesantes aplicaciones en diferentes temas. Estas incluyen, entre otras:

• La famosa identidad de Euler
• La forma exponencial de los números complejos
• Definiciones alternativas de funciones trigonométricas e hiperbólicas
• Generalización de funciones exponenciales y logarítmicas a números complejos
• Demostraciones alternativas del teorema de De Moivre y las identidades trigonométricas aditivas

La identidad de Euler

La identidad de Euler es frecuentemente considerada como la ecuación más hermosa en las matemáticas. Se expresa como

eiπ+1=0

donde exhibe cinco de las constantes más importantes en matemáticas. Estas son:

• El elemento neutro de la suma 0
• La unidad 1
• La constante Pi π (razón entre la circunferencia de un círculo y su diámetro)
• La base del logaritmo natural e
• La unidad imaginaria i

Entre estas, se representan tres tipos de números: enteros, números irracionales y números imaginarios. También se representan tres de las operaciones matemáticas básicas: adición, multiplicación y exponenciación.

Obtenemos la identidad de Euler partiendo de la fórmula de Euler eix=cos⁡x+isin⁡x y estableciendo x=π y trasladando el subsiguiente −1 al lado izquierdo de la ecuación. La fórmula intermedia eiπ=−1 es común en el contexto del círculo unitario trigonométrico en el plano complejo: corresponde al punto en el círculo unitario cuyo ángulo con respecto al eje real positivo es π.

Números complejos en forma exponencial

En este punto, ya sabemos que un número complejo z puede ser expresado en coordenadas cartesianas como x+iy, donde x e y son respectivamente la parte real y la parte imaginaria de z.

En efecto, el mismo número complejo puede ser expresado también en coordenadas polares como r(cos⁡θ+isin⁡θ), donde r es la magnitud de su distancia al origen, y θ es su ángulo con respecto al eje real positivo.

Pero no termina ahí: gracias a la fórmula de Euler, todo número complejo puede ahora ser expresado como un exponencial complejo de la siguiente manera:

z=r(cos⁡θ+isin⁡θ)=reiθ

donde r y θ son los mismos números que antes.

Para ir de (x,y) a (r,θ), utilizamos las fórmulas r=x2+y2θ=atan2⁡(y,x) (donde atan2⁡(y,x) es la función arcotangente de dos argumentos con atan2⁡(y,x)=arctan⁡(yx) siempre que x>0.)

A la inversa, para ir de (r,θ) a (x,y), utilizamos las fórmulas: x=rcos⁡θy=rsin⁡θ La forma exponencial de los números complejos también facilita la multiplicación de números complejos — de manera similar a como las coordenadas rectangulares facilitan la suma. Por ejemplo, dados dos números complejos z1=r1eiθ1 y z2=r2eiθ2, ahora podemos multiplicarlos de la siguiente manera: z1z2=r1eiθ1⋅r2eiθ2=r1r2ei(θ1+θ2) En el mismo espíritu, también podemos dividir los mismos dos números de la siguiente manera: z1z2=r1eiθ1r2eiθ2=r1r2ei(θ1−θ2)

Si hubiéramos utilizado la notación rectangular x+iy en su lugar, la misma división habría requerido multiplicar por el conjugado complejo en el numerador y denominador. Con las coordenadas polares, la situación habría sido la misma (quizás incluso peor).

En todo caso, la forma exponencial ciertamente facilita ver que multiplicar dos números complejos es realmente lo mismo que multiplicar magnitudes y sumar ángulos, y que dividir dos números complejos es realmente lo mismo que dividir magnitudes y restar ángulos.

Definiciones alternativas de funciones clave

La fórmula de Euler también puede ser utilizada para proporcionar definiciones alternativas a funciones clave como la función exponencial compleja, funciones trigonométricas como el seno, coseno y tangente, y sus contrapartes hiperbólicas. También puede ser utilizada para establecer la relación entre algunas de estas funciones.

Función exponencial compleja

Para comenzar, recordemos que la fórmula de Euler establece que eix=cos⁡x+isin⁡x Si se asume que la fórmula se mantiene solo para x real, entonces la función exponencial está definida únicamente hasta los números imaginarios. Sin embargo, también podemos expandir la función exponencial para incluir todos los números complejos — siguiendo un truco muy simple:

ez=ex+iy(=exeiy)=dfex(cos⁡y+isin⁡y)

En otras palabras, el exponencial del número complejo x+iy es simplemente el número complejo cuya magnitud es ex y cuyo ángulo es y. Resulta interesante que esto implica que el exponencial complejo esencialmente mapea líneas verticales a círculos. He aquí una animación para ilustrar este punto:

Funciones Trigonométricas

Además de extender el dominio de la función exponencial, podemos utilizar la fórmula de Euler para derivar una ecuación similar para el ángulo opuesto −x: e−ix=cos⁡x−isin⁡x. Esta ecuación, junto con la fórmula de Euler en sí, constituyen un sistema de ecuaciones del cual podemos aislar tanto las funciones seno como coseno.

Por ejemplo, al restar la ecuación e−ix de la ecuación eix, los cosenos se cancelan y, tras dividir por 2i, obtenemos la forma exponencial compleja de la función seno:

sin⁡x=eix−e−ix2i

De manera similar, al sumar las dos ecuaciones, los senos se cancelan y, tras dividir por 2, obtenemos la forma exponencial compleja de la función coseno:

cos⁡x=eix+e−ix2

Para confirmar, he aquí un vídeo que ilustra las mismas derivaciones con mayor detalle.

Por otro lado, la función tangente se define como sin⁡xcos⁡x, por lo que en términos de exponenciales complejas, se convierte en:

tan⁡x=eix−e−ixi(eix+e−ix)

Si se demuestra que la fórmula de Euler es válida para todos los números complejos (como lo hicimos en la demostración mediante series de potencias), entonces lo mismo sería cierto para estas tres fórmulas. Su presencia nos permite alternar libremente entre funciones trigonométricas y exponenciales complejas, lo cual es una gran ventaja cuando se trata de calcular derivadas e integrales.

Funciones Hiperbólicas

Además de las funciones trigonométricas, las funciones hiperbólicas son otra clase de funciones que pueden definirse en términos de exponenciales complejas. De hecho, es a través de esta conexión que podemos identificar una función hiperbólica con su contraparte trigonométrica.

Por ejemplo, comenzando con el seno complejo y el coseno complejo y sustituyendo iz (y haciendo uso de los hechos de que i2=−1 y 1/i=−i), tenemos: sin⁡iz=ei(iz)−e−i(iz)2i=e−z−ez2i=i(ez−e−z2)=isinh⁡z cos⁡iz=ei(iz)+e−i(iz)2=ez+e−z2=cosh⁡z A partir de esto, también podemos sustituir iz en la tangente compleja y obtener: tan⁡(iz)=sin⁡izcos⁡iz=isinh⁡zcosh⁡z=itanh⁡z En resumen, esto significa que ahora podemos definir las funciones hiperbólicas en términos de funciones trigonométricas de la siguiente manera:

sinh⁡z=sin⁡izi cosh⁡z=cos⁡iz tanh⁡z=tan⁡izi

Sin embargo, estas no son las únicas funciones a las que podemos proporcionar nuevas definiciones. De hecho, el logaritmo complejo y el exponencial complejo general son otras dos clases de funciones que podemos definir como resultado de la fórmula de Euler.

Logaritmo Complejo y Exponencial Complejo General

El logaritmo de un número complejo se comporta de manera peculiar en comparación con el logaritmo de un número real. Más específicamente, tiene un número infinito de valores en lugar de uno.

Para ver cómo, comenzamos con la definición de la función logarítmica como la inversa de la función exponencial. Es decir: eln⁡z=z ln⁡(ez)=z Además, también sabemos que para cualquier par de números complejos z1 y z2, la propiedad aditiva de los exponentes se mantiene: ez1ez2=ez1+z2 Así, cuando un número complejo no nulo se expresa como un exponencial, tenemos que: z=|z|eiϕ=eln⁡|z|eiϕ=eln⁡|z|+iϕ donde |z| es la magnitud de z y ϕ es el ángulo de z desde el eje real positivo. Y dado que el logaritmo es simplemente el exponente de un número cuando se eleva a e, se establece la siguiente definición: ln⁡z=ln⁡|z|+iϕ A primera vista, esto parece una forma robusta de definir el logaritmo complejo. Sin embargo, una segunda mirada revela que el logaritmo definido de esta manera puede asumir un número infinito de valores, debido al hecho de que ϕ también puede elegirse como cualquier otro número de la forma ϕ+2πk (donde k es un entero).

Por ejemplo, hemos visto anteriormente que e0=1 y e2πi=1. Esto significa que uno podría definir el logaritmo de 1 como 0 y 2πi, o cualquier número de la forma 2πki (donde k es un entero).

Para resolver este enigma, se suelen utilizar dos enfoques distintos. El primer enfoque consiste en considerar el logaritmo complejo simplemente como una función multivaluada. Es decir, una función que asocia cada entrada a un conjunto de valores. Una manera de lograrlo es definir ln⁡z de la siguiente forma:{ln⁡|z|+i(ϕ+2πk)}donde −π<ϕ≤π y k es un número entero. En este caso, la cláusula −π<ϕ≤π tiene el efecto de restringir el ángulo de z a un único candidato. Debido a esto, el ϕ definido de esta manera se denomina habitualmente el ángulo principal de z.

El segundo enfoque, que podría considerarse más elegante, consiste simplemente en definir el logaritmo complejo de z de manera que ϕ sea el ángulo principal de z. Con esta interpretación, la definición original se convierte entonces en bien definida:

ln⁡z=ln⁡|z|+iϕ

Por ejemplo, bajo esta nueva regla, tendríamos que ln⁡1=0 y ln⁡i=ln⁡(eiπ2)=iπ2. ¡Ya no nos enfrentamos al problema de la periodicidad de los ángulos!

Sin embargo, con la restricción de que −π<ϕ≤π, el rango del logaritmo complejo se reduce ahora a la región rectangular −π<y≤π (es decir, la rama principal). Y si deseamos preservar la relación inversa entre el logaritmo y la función exponencial, también necesitaríamos hacer lo mismo con el dominio de la función exponencial.

No obstante, dado que el logaritmo complejo está ahora bien definido, también podemos definir muchas otras cosas basadas en él sin incurrir en ambigüedades. Un ejemplo de ello sería la exponencial compleja general (con una base a no nula), que puede definirse de la siguiente manera:

az=eln⁡(az)=dfezln⁡a

Por ejemplo, utilizando la exponencial compleja general tal como se ha definido anteriormente, ahora podemos comprender el significado de ii:ii=eiln⁡i=eiπ2i=e−π2≈0,208

Demostraciones Alternativas del Teorema de De Moivre y las Identidades Trigonométricas Aditivas

El teorema conocido como teorema de De Moivre establece que

(cos⁡x+isin⁡x)n=cos⁡nx+isin⁡nx

donde x es un número real y n es un número entero. Por defecto, esto puede demostrarse mediante inducción (utilizando algunas identidades trigonométricas), pero con la ayuda de la fórmula de Euler, ahora existe una demostración mucho más simple.

Para empezar, recordemos que la propiedad multiplicativa de los exponentes establece que(ez)k=ezkAunque esta propiedad generalmente no es cierta para números complejos, sí se cumple en el caso especial en que k es un número entero. De hecho, no es difícil ver que en este caso, las matemáticas se reducen esencialmente a aplicaciones repetidas de la propiedad aditiva de los exponentes.

Y con esto establecido, podemos derivar fácilmente el teorema de De Moivre de la siguiente manera:(cos⁡x+isin⁡x)n=(eix)n=einx=cos⁡nx+isin⁡nxEn la práctica, este teorema se utiliza comúnmente para encontrar las raíces de un número complejo, y para obtener expresiones cerradas para sin⁡nx y cos⁡nx. Lo hace reduciendo funciones elevadas a altas potencias a funciones trigonométricas simples, de modo que los cálculos puedan realizarse con facilidad.

De hecho, el teorema de De Moivre no es el único teorema cuya demostración puede simplificarse como resultado de la fórmula de Euler. Otras identidades, como las identidades aditivas para sin⁡(x+y) y cos⁡(x+y), también se benefician de este efecto.

En efecto, ya sabemos que para todos los números reales x e y:cos⁡(x+y)+isin⁡(x+y)=ei(x+y)=eix⋅eiy=(cos⁡x+isin⁡x)(cos⁡y+isin⁡y)=(cos⁡xcos⁡y−sin⁡xsin⁡y)+i(sin⁡xcos⁡y+cos⁡xsin⁡y)Una vez aquí, igualar las partes real e imaginaria en ambos lados produce las célebres identidades que buscábamos:

cos⁡(x+y)=cos⁡xcos⁡y−sin⁡xsin⁡ysin⁡(x+y)=sin⁡xcos⁡y+cos⁡xsin⁡y

Conclusión

Como se puede observar, la fórmula de Euler es una joya rara en el ámbito de las matemáticas. Establece la relación fundamental entre las funciones exponenciales y trigonométricas, y allana el camino para un gran desarrollo en el mundo de los números complejos, las funciones complejas y la teoría relacionada.

En efecto, ya sea la identidad de Euler o el logaritmo complejo, la fórmula de Euler parece no dejar piedra sin remover cuando se trata de expresiones que involucran sin, i y e. Es una herramienta poderosa cuyo dominio puede ser tremendamente gratificante, y por esa razón es una candidata legítima a “la fórmula más notable de las matemáticas“.

Identidad de Eulereiπ+1=0
Número complejo (forma exponencial)z=reiθ
Exponencial complejaex+iy=ex(cos⁡y+isin⁡y)
Seno (forma exponencial)sin⁡x=eix−e−ix2i
Coseno (forma exponencial)cos⁡x=eix+e−ix2
Tangente (forma exponencial)tan⁡x=eix−e−ixi(eix+e−ix)
Seno hiperbólico (forma exponencial)sinh⁡z=sin⁡izi
Coseno hiperbólico (forma exponencial)cosh⁡z=cos⁡iz
Tangente hiperbólica (forma exponencial)tanh⁡z=tan⁡izi
Logaritmo complejoln⁡z=ln⁡|z|+iϕ
Exponencial compleja generalaz=ezln⁡a
Teorema de De Moivre(cos⁡x+isin⁡x)n=cos⁡nx+isin⁡nx
Identidad aditiva del senosin⁡(x+y)=sin⁡xcos⁡y+cos⁡xsin⁡y
Identidad aditiva del cosenocos⁡(x+y)=cos⁡xcos⁡y−sin⁡xsin⁡y

Descripción	Enunciado
Fórmula de Euler	eix=cos⁡x+isin⁡x

Fuentes

• Matemáticas para Físicos (Susan M. Lea)
• Manual de Cambridge de Fórmulas de Física (Graham Woan)