La identidad de Euler es frecuentemente aclamada como la fórmula más bella de las matemáticas. Las personas la portan en camisetas y se la tatúan en el cuerpo. ¿Por qué?
La identidad se expresa como
![[ e^{ipi }+1=0, ]](https://plus.maths.org/MI/17eab3c768113bf642698c4da7edf422/images/img-0001.png) |
 Leonhard Euler, 1707-1783. Retrato de Johann Georg Brucker.
Leonhard Euler, 1707-1783. Retrato de Johann Georg Brucker.
donde 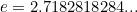 es la base del logaritmo natural,
es la base del logaritmo natural, 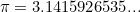 es la razón entre la circunferencia y el diámetro de un círculo, y
es la razón entre la circunferencia y el diámetro de un círculo, y 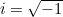 . Estas tres constantes son extremadamente importantes en matemáticas, y dado que la identidad también involucra
. Estas tres constantes son extremadamente importantes en matemáticas, y dado que la identidad también involucra  y
y  , tenemos una fórmula que conecta cinco de los números más importantes en matemáticas utilizando cuatro de las operaciones y relaciones matemáticas más importantes: adición, multiplicación, exponenciación e igualdad. He aquí el motivo por el cual los matemáticos aprecian tanto la identidad de Euler.
, tenemos una fórmula que conecta cinco de los números más importantes en matemáticas utilizando cuatro de las operaciones y relaciones matemáticas más importantes: adición, multiplicación, exponenciación e igualdad. He aquí el motivo por el cual los matemáticos aprecian tanto la identidad de Euler.
Pero, ¿de dónde proviene y qué significa? Como mencionamos anteriormente, 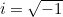 . Esto puede parecer sorprendente porque los números negativos no deberían tener raíces cuadradas. Sin embargo, si simplemente decretamos que
. Esto puede parecer sorprendente porque los números negativos no deberían tener raíces cuadradas. Sin embargo, si simplemente decretamos que 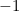 sí tiene una raíz cuadrada y la denominamos
sí tiene una raíz cuadrada y la denominamos 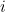 , entonces podemos construir una clase completamente nueva de números, llamados números complejos. Los números complejos tienen la forma
, entonces podemos construir una clase completamente nueva de números, llamados números complejos. Los números complejos tienen la forma 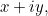 donde
donde  y
y 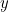 son números reales ordinarios (para el número complejo
son números reales ordinarios (para el número complejo 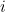 tenemos
tenemos 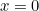 y
y 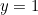 ). Véase aquí para una breve introducción a los números complejos y cómo calcular con ellos. Nótese que un número real también puede ser considerado como un número complejo. El número
). Véase aquí para una breve introducción a los números complejos y cómo calcular con ellos. Nótese que un número real también puede ser considerado como un número complejo. El número 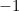 , por ejemplo, es un número complejo con
, por ejemplo, es un número complejo con 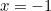 y
y 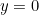 .
.
Así como un número real está representado por un punto en una recta numérica, un número complejo  está representado por un punto en el plano. Al número complejo
está representado por un punto en el plano. Al número complejo 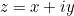 le asociamos el punto con coordenadas
le asociamos el punto con coordenadas 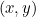 .
.
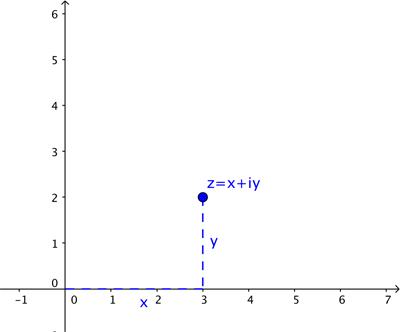
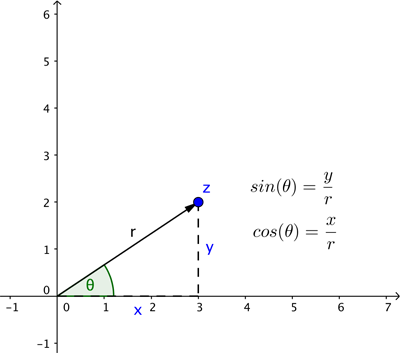
En esta descripción utilizamos coordenadas cartesianas: estas describen la ubicación de un punto indicándonos cuánto avanzar en la dirección horizontal y cuánto en la dirección vertical. Sin embargo, en ocasiones resulta más conveniente describir la ubicación de un punto en términos del vector que parte del punto de intersección de los dos ejes, como se muestra a continuación.
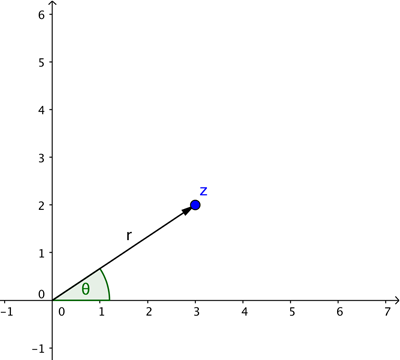
Para definir ese vector se necesita su longitud  y el ángulo
y el ángulo 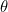 que forma con el eje
que forma con el eje  positivo (medido en sentido antihorario). Estas son las coordenadas polares de nuestro punto. La trigonometría básica (véase el diagrama a continuación) nos indica que si un punto tiene coordenadas cartesianas
positivo (medido en sentido antihorario). Estas son las coordenadas polares de nuestro punto. La trigonometría básica (véase el diagrama a continuación) nos indica que si un punto tiene coordenadas cartesianas 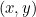 y coordenadas polares
y coordenadas polares 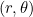 , entonces
, entonces
![[ x=r cos {( heta )} ]](https://plus.maths.org/MI/37f3a5d111741224a911781164a3c4b7/images/img-0006.png) |
y
![[ y=r sin {( heta )}. ]](https://plus.maths.org/MI/37f3a5d111741224a911781164a3c4b7/images/img-0007.png) |
Por lo tanto, el número complejo  representado por nuestro punto,
representado por nuestro punto, 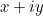 , también puede escribirse como
, también puede escribirse como
![[ z= r (cos {( heta )}+isin {( heta )}). ]](https://plus.maths.org/MI/c9570eacdeb0833cf294aca44d62bf7e/images/img-0003.png) |
Aquí viene el punto crucial. Resulta que para números reales  y
y 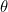
![[ r(cos {( heta )} + i sin {( heta )}) = re^{i heta }. ]](https://plus.maths.org/MI/c9570eacdeb0833cf294aca44d62bf7e/images/img-0006.png) |
Esto puede demostrarse utilizando series de potencias, véase aquí para obtener más información. Es un hecho hermoso que la función exponencial y las dos funciones trigonométricas seno y coseno estén vinculadas de esta manera. Y significa que cualquier número complejo  puede escribirse como
puede escribirse como 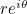 donde
donde  es la longitud de la línea que conecta el punto en el plano asociado a
es la longitud de la línea que conecta el punto en el plano asociado a  al punto de intersección de los ejes, y
al punto de intersección de los ejes, y 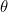 es el ángulo que forma dicha línea con el eje
es el ángulo que forma dicha línea con el eje  positivo (medido en sentido antihorario).
positivo (medido en sentido antihorario).
Esto ahora hace que la identidad de Euler sea cristalina. El número complejo 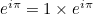 representa el punto en el plano a una distancia
representa el punto en el plano a una distancia  del punto de intersección de los ejes con un ángulo asociado de
del punto de intersección de los ejes con un ángulo asociado de 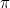 . Ese es el punto con coordenadas cartesianas
. Ese es el punto con coordenadas cartesianas 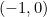 que representa el número complejo
que representa el número complejo 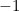 .
.
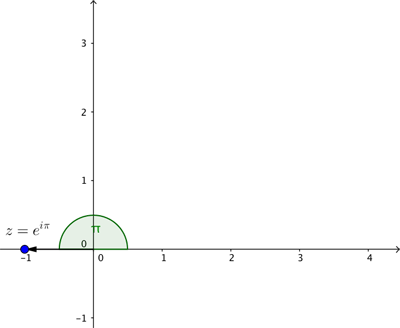
Reuniendo todos estos elementos, observamos que
![\[ e^{i\pi } = -1, \]](https://plus.maths.org/MI/b7b172cee37d9c06da34d769912d2d57/images/img-0001.png) |
lo cual significa que
![\[ e^{i\pi }+1 = 0. \]](https://plus.maths.org/MI/b7b172cee37d9c06da34d769912d2d57/images/img-0002.png) |
Y esa es la identidad de Euler.












