Euler’s identity is often hailed as the most beautiful formula in mathematics. People wear it on T-shirts and get it tattooed on their bodies. Why?
The identity reads
![\[ e^{i\pi }+1=0, \]](https://plus.maths.org/MI/17eab3c768113bf642698c4da7edf422/images/img-0001.png) |
Leonhard Euler, 1707-1783. Portrait by Johann Georg Brucker.
where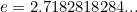 
is the base of the natural logarithm, 
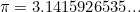is the ratio between a circle’s circumference and diameter, and 
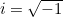. These three constants are extremely important in maths — and since the identity also involves 
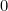and 
, we have a formula that connects five of the most important numbers in mathematics using four of the most important mathematical operations and relations – addition, multiplication, exponentiation and equality. That’s why mathematicians love Euler’s identity so much.
But where does it come from and what does it mean? As we mentioned above,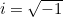 
. This might seem shocking because negative numbers are not supposed to have square roots. However, if we simply decree that 
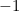does have a square root and call it 
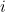, then we can build a whole new class of numbers, called the complex numbers. Complex numbers have the form 
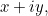where 
and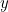 
are ordinary real numbers (for the complex number 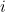we have 
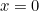and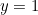 
). See here for a quick introduction to complex numbers and how to calculate with them. Note that a real number can also be viewed as a complex number. The number 
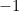, for example, is a complex number with 
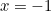and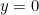 
.
Just like a real number is represented by a point on a number line, a complex number 
is represented by a point on the plane. To the complex number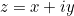 
we associate the point with coordinates 
.
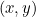In this description we used Cartesian coordinates: they describe the location of a point by telling you how far to walk along the horizontal direction and how far to walk along the vertical direction. Sometimes, however, it’s more convenient to describe the location of a point in terms of the arrow starting at the crossing point of the two axes as shown below.
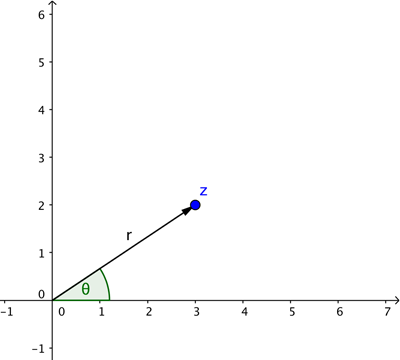
To define that arrow you need its length 
and the angle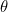 
it makes with the positive 
-axis (measured anti-clockwise). These are the polar coordinates of our point. Basic trigonometry (see the diagram below) tells us that if a point has Cartesian coordinates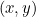 
and polar coordinates 
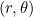, then
![\[ x=r \cos {(\theta )} \]](https://plus.maths.org/MI/37f3a5d111741224a911781164a3c4b7/images/img-0006.png) |
and
![\[ y=r \sin {(\theta )}. \]](https://plus.maths.org/MI/37f3a5d111741224a911781164a3c4b7/images/img-0007.png) |
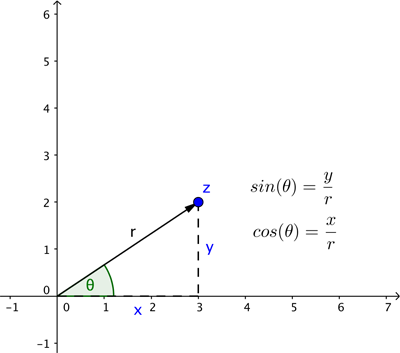
Therefore the complex number 
represented by our point,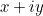 
, can also be written as
![\[ z= r (\cos {(\theta )}+i\sin {(\theta )}). \]](https://plus.maths.org/MI/c9570eacdeb0833cf294aca44d62bf7e/images/img-0003.png) |
Here comes the crucial point. It just so happens that for real numbers 
and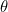 
![\[ r(\cos {(\theta )} + i \sin {(\theta )}) = re^{i\theta }. \]](https://plus.maths.org/MI/c9570eacdeb0833cf294aca44d62bf7e/images/img-0006.png) |
You can prove this using power series, see here to find out more. It’s a beautiful fact that the exponential function and the two trigonometric functions sine and cosine are linked in this way. And it means that any complex number 
can be written as 
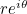where 
is the length of the line connecting the point on the plane that is associated to to the crossing point of the axes, and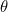 
is the angle that line makes with the positive 
-axis (measured anti-clockwise).
This now makes Euler’s identity crystal clear. The complex number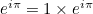 
represents the point on the plane at distance 
from the crossing point of the axes with an associated angle of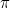 
. That’s the point with Cartesian coordinates 
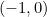which represents the complex number 
.
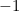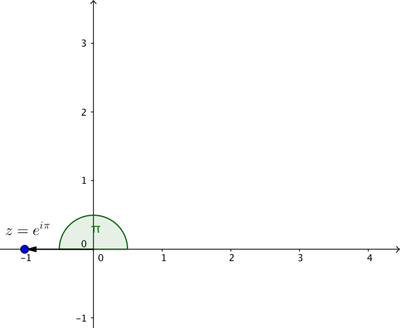
Putting all this together, we see that
![\[ e^{i\pi } = -1, \]](https://plus.maths.org/MI/b7b172cee37d9c06da34d769912d2d57/images/img-0001.png) |
which means that
![\[ e^{i\pi }+1 = 0. \]](https://plus.maths.org/MI/b7b172cee37d9c06da34d769912d2d57/images/img-0002.png) |
And that’s Euler’s identity.
