Euler’s identiteit wordt vaak gezien als de mooiste formule in de wiskunde. Mensen dragen het op T-shirts en laten het zelfs tatoeëren. Waarom?
De identiteit luidt
![[ e^{ipi }+1=0, ]](https://plus.maths.org/MI/17eab3c768113bf642698c4da7edf422/images/img-0001.png) |
 Leonhard Euler, 1707-1783. Portret door Johann Georg Brucker.
Leonhard Euler, 1707-1783. Portret door Johann Georg Brucker.
waarbij 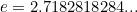 het grondgetal van de natuurlijke logaritme is,
het grondgetal van de natuurlijke logaritme is, 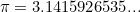 de verhouding tussen de omtrek en diameter van een cirkel, en
de verhouding tussen de omtrek en diameter van een cirkel, en 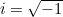 . Deze drie constanten zijn extreem belangrijk in de wiskunde – en omdat de identiteit ook
. Deze drie constanten zijn extreem belangrijk in de wiskunde – en omdat de identiteit ook  en
en  bevat, hebben we een formule die vijf van de belangrijkste getallen in de wiskunde verbindt met vier van de belangrijkste wiskundige bewerkingen en relaties – optelling, vermenigvuldiging, machtsverheffen en gelijkheid. Daarom zijn wiskundigen zo gek op Euler’s identiteit.
bevat, hebben we een formule die vijf van de belangrijkste getallen in de wiskunde verbindt met vier van de belangrijkste wiskundige bewerkingen en relaties – optelling, vermenigvuldiging, machtsverheffen en gelijkheid. Daarom zijn wiskundigen zo gek op Euler’s identiteit.
Maar waar komt het vandaan en wat betekent het? Zoals we hierboven al zeiden, 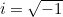 . Dit kan schokkend lijken omdat negatieve getallen geen wortels horen te hebben. Maar als we simpelweg besluiten dat
. Dit kan schokkend lijken omdat negatieve getallen geen wortels horen te hebben. Maar als we simpelweg besluiten dat 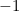 wel een wortel heeft en het
wel een wortel heeft en het 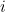 noemen, dan kunnen we een hele nieuwe klasse getallen bouwen, genaamd de complexe getallen. Complexe getallen hebben de vorm
noemen, dan kunnen we een hele nieuwe klasse getallen bouwen, genaamd de complexe getallen. Complexe getallen hebben de vorm 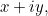 waarbij
waarbij  en
en 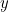 gewone reële getallen zijn (voor het complexe getal
gewone reële getallen zijn (voor het complexe getal 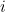 hebben we
hebben we 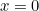 en
en 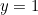 ). Kijk hier voor een snelle intro over complexe getallen en hoe je ermee rekent. Let op dat een reëel getal ook gezien kan worden als een complex getal. Het getal
). Kijk hier voor een snelle intro over complexe getallen en hoe je ermee rekent. Let op dat een reëel getal ook gezien kan worden als een complex getal. Het getal 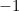 is bijvoorbeeld een complex getal met
is bijvoorbeeld een complex getal met 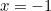 en
en 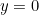 .
.
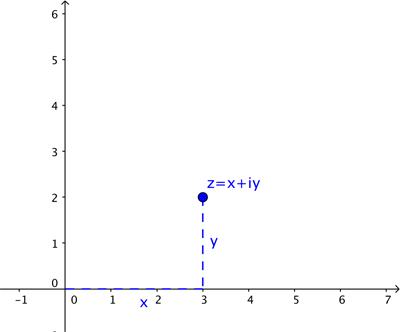
Net zoals een reëel getal wordt weergegeven door een punt op een getallenlijn, wordt een complex getal  weergegeven door een punt in het vlak. Bij het complexe getal
weergegeven door een punt in het vlak. Bij het complexe getal 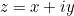 hoort het punt met coördinaten
hoort het punt met coördinaten 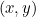 .
.
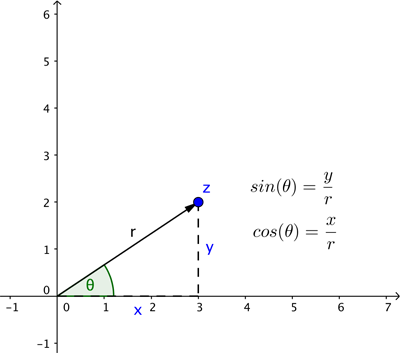
In deze beschrijving gebruikten we Cartesische coördinaten: ze beschrijven de locatie van een punt door te vertellen hoe ver je horizontaal en verticaal moet lopen. Soms is het echter handiger om de locatie van een punt te beschrijven in termen van de pijl die begint bij het snijpunt van de twee assen, zoals hieronder getoond.
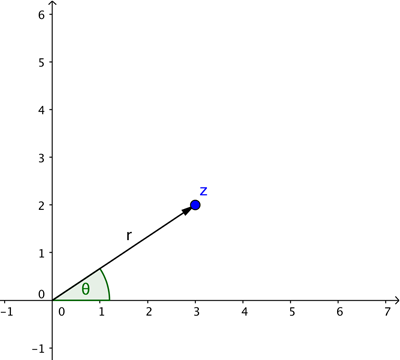
Om die pijl te definiëren heb je de lengte  nodig en de hoek
nodig en de hoek 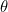 die hij maakt met de positieve
die hij maakt met de positieve  -as (tegen de klok in gemeten). Dit zijn de poolcoördinaten van ons punt. Basis trigonometrie (zie het diagram hieronder) vertelt ons dat als een punt Cartesische coördinaten
-as (tegen de klok in gemeten). Dit zijn de poolcoördinaten van ons punt. Basis trigonometrie (zie het diagram hieronder) vertelt ons dat als een punt Cartesische coördinaten 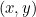 heeft en poolcoördinaten
heeft en poolcoördinaten 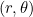 , dan geldt
, dan geldt
![[ x=r cos {( heta )} ]](https://plus.maths.org/MI/37f3a5d111741224a911781164a3c4b7/images/img-0006.png) |
en
![[ y=r sin {( heta )}. ]](https://plus.maths.org/MI/37f3a5d111741224a911781164a3c4b7/images/img-0007.png) |
Daarom kan het complexe getal  dat door ons punt wordt weergegeven,
dat door ons punt wordt weergegeven, 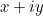 , ook geschreven worden als
, ook geschreven worden als
![[ z= r (cos {( heta )}+isin {( heta )}). ]](https://plus.maths.org/MI/c9570eacdeb0833cf294aca44d62bf7e/images/img-0003.png) |
Hier komt het cruciale punt. Het blijkt dat voor reële getallen  en
en 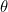
![[ r(cos {( heta )} + i sin {( heta )}) = re^{i heta }. ]](https://plus.maths.org/MI/c9570eacdeb0833cf294aca44d62bf7e/images/img-0006.png) |
Je kunt dit bewijzen met machtreeksen, kijk hier voor meer info. Het is een prachtig feit dat de exponentiële functie en de twee trigonometrische functies sinus en cosinus op deze manier verbonden zijn. En het betekent dat elk complex getal  geschreven kan worden als
geschreven kan worden als 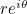 waarbij
waarbij  de lengte is van de lijn die het punt in het vlak verbindt dat geassocieerd is met
de lengte is van de lijn die het punt in het vlak verbindt dat geassocieerd is met  naar het snijpunt van de assen, en
naar het snijpunt van de assen, en 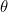 is de hoek die de lijn maakt met de positieve
is de hoek die de lijn maakt met de positieve  -as (tegen de klok in gemeten).
-as (tegen de klok in gemeten).
Dit maakt de identiteit van Euler nu glashelder. Het complexe getal 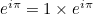 stelt het punt op het vlak voor op afstand
stelt het punt op het vlak voor op afstand  van het snijpunt van de assen met een bijbehorende hoek van
van het snijpunt van de assen met een bijbehorende hoek van 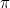 . Dat is het punt met Cartesiaanse coördinaten
. Dat is het punt met Cartesiaanse coördinaten 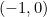 dat het complexe getal
dat het complexe getal 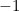 voorstelt.
voorstelt.
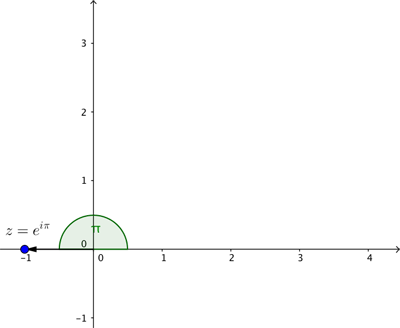
Als we dit allemaal bij elkaar optellen, zien we dat
![[ e^{ipi } = -1, ]](https://plus.maths.org/MI/b7b172cee37d9c06da34d769912d2d57/images/img-0001.png) |
wat betekent dat
![[ e^{ipi }+1 = 0. ]](https://plus.maths.org/MI/b7b172cee37d9c06da34d769912d2d57/images/img-0002.png) |
En dat is de identiteit van Euler.












