Over de formule van Euler

In de wereld van complexe getallen, als we trigonometrische uitdrukkingen integreren, komen we waarschijnlijk de zogenaamde formule van Euler tegen.

Vernoemd naar de legendarische wiskundige Leonhard Euler, verdient deze krachtige vergelijking een nadere beschouwing — zodat we ‘m optimaal kunnen gebruiken.

We gaan kijken hoe de formule van Euler ons in staat stelt om complexe getallen uit te drukken als exponentiëlen, en we verkennen de verschillende manieren waarop het relatief eenvoudig kan worden vastgesteld.

Daarnaast zullen we ook kijken naar verschillende toepassingen zoals het specifieke geval van Eulers identiteit, de exponentiële vorm van complexe getallen, alternatieve definities van belangrijke functies, en alternatieve bewijzen van de stelling van de Moivre en trigonometrische optelformules.

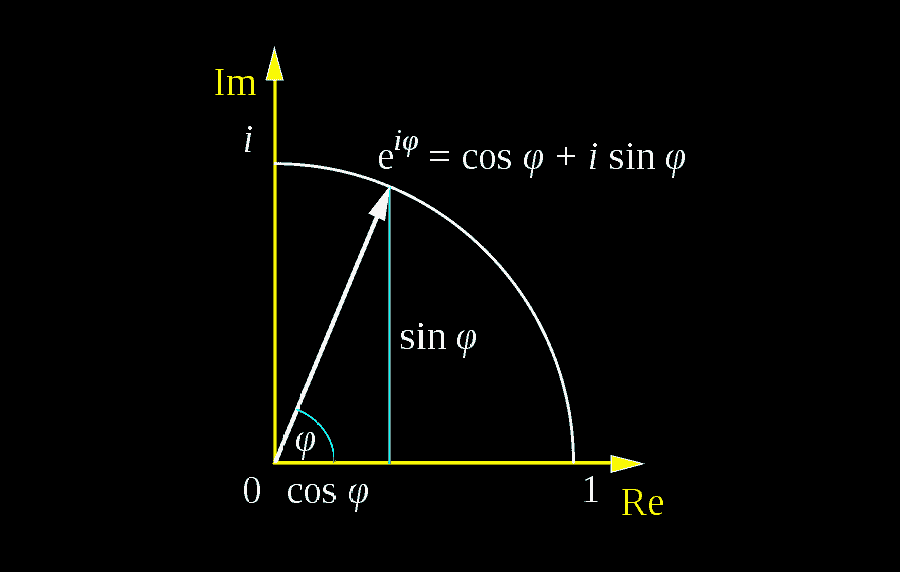
De formule van Euler uitgelegd: Introductie, interpretatie en voorbeelden

Dus wat is de formule van Euler precies? Kort gezegd is het de stelling die stelt dat

eix=cos⁡x+isin⁡x

waarbij:

• x een reëel getal is.
• e het grondgetal van de natuurlijke logaritme is.
• i de imaginaire eenheid is (oftewel de vierkantswortel van −1).

De formule van Euler legt de fundamentele relatie vast tussen trigonometrische functies en exponentiële functies. Geometrisch kan het worden gezien als een manier om twee representaties van hetzelfde complexe eenheidsgetal in het complexe vlak te overbruggen.

Laten we eens kijken naar enkele belangrijke waarden van de formule van Euler, en zien hoe ze overeenkomen met punten in de trigonometrische cirkel/eenheidscirkel:

• Voor x=0 hebben we e0=cos⁡0+isin⁡0, wat 1=1 oplevert. Tot zover goed: we weten dat een hoek van 0 op de trigonometrische cirkel 1 is op de reële as, en dat is wat we hier krijgen.
• Voor x=1 hebben we ei=cos⁡1+isin⁡1. Dit resultaat suggereert dat ei precies het punt op de eenheidscirkel is waarvan de hoek 1 radiaal is.
• Voor x=π2 hebben we eiπ2=cos⁡π2+isin⁡π2=i. Dit resultaat is nuttig bij sommige berekeningen die gerelateerd zijn aan natuurkunde.
• Voor x=π hebben we eiπ=cos⁡π+isin⁡π, wat betekent dat eiπ=−1. Dit resultaat is equivalent aan de beroemde identiteit van Euler.
• Voor x=2π hebben we ei(2π)=cos⁡2π+isin⁡2π, wat betekent dat ei(2π)=1, hetzelfde als bij x=0.

Een belangrijke sleutel om Euler’s formule te snappen, is om ‘m als volgt te herschrijven:(ei)x=cos⁡x+isin⁡xwaar:

• De rechterkant kan je zien als het complexe getal met lengte 1 en hoek x.
• De linkerkant kan je zien als het complexe getal met lengte 1 en hoek 1 radiaal tot de macht x.

En aangezien een complex getal met lengte 1 tot een macht verheffen gezien kan worden als herhaaldelijk vermenigvuldigen (oftewel, hoeken optellen in dit geval), kan Euler’s formule gezien worden als twee verschillende manieren om rond de eenheidscirkel te lopen en op hetzelfde punt uit te komen.

Afleidingen

Euler’s formule kan op minstens drie manieren worden afgeleid. De eerste afleiding is gebaseerd op machtreeksen, waarbij de exponentiële, sinus en cosinus functies worden uitgeschreven als machtreeksen om te concluderen dat de formule inderdaad klopt.

De tweede afleiding van Euler’s formule is gebaseerd op calculus, waarbij beide kanten van de vergelijking als functies worden behandeld en dienovereenkomstig worden gedifferentieerd. Dit leidt dan tot de identificatie van een gemeenschappelijke eigenschap – eentje die kan worden gebruikt om aan te tonen dat beide functies inderdaad gelijk zijn.

Nog een andere afleiding van Euler’s formule maakt gebruik van poolcoördinaten in het complexe vlak, waardoor de waarden van r en θ vervolgens worden gevonden. Sterker nog, je kunt misschien wel raden wat deze waarden zijn – gewoon door naar de formule zelf te kijken!

Afleiding 1: Machtreeksen

Een van de meest intuïtieve afleidingen van Euler’s formule maakt gebruik van machtreeksen. Het bestaat uit het uitbreiden van de machtreeksen van exponentieel, sinus en cosinus – om uiteindelijk te concluderen dat de gelijkheid geldt.

Als kanttekening, deze aanpak gaat ervan uit dat de machtreeksuitbreidingen van sin⁡z, cos⁡z, en ez absoluut convergent zijn overal (bijvoorbeeld dat ze gelden voor alle complexe getallen z). Het heeft echter ook het voordeel dat het laat zien dat Euler’s formule ook geldt voor alle complexe getallen z.

Voor een complexe variabele z is de machtreeksuitbreiding van ez:ez=1+z1!+z22!+z33!+z44!+⋯Laten we nu z nemen als ix (waarbij x een willekeurig complex getal is). Als z tot hogere machten wordt verheven, wordt i ook tot hogere machten verheven. De eerste acht machten van i zien er zo uit:(volgens de definitie van )i0=1i4=i2⋅i2=1i1=ii5=i⋅i4=ii2=−1(volgens de definitie van i)i6=i⋅i5=−1i3=i⋅i2=−ii7=i⋅i6=−i(merk de cyclische aard van de machten van i op: 1, i, −1, −i. We zullen deze machten zo meteen gebruiken.)

Met z=ix wordt de uitbreiding van ez:eix=1+ix+(ix)22!+(ix)33!+(ix)44!+⋯Als we de machten van i eruit halen, krijgen we:eix=1+ix−x22!−ix33!+x44!+ix55!−x66!−ix77!+x88!+⋯En aangezien de machtreeksuitbreiding van ez absoluut convergent is, kunnen we de termen herschikken zonder de waarde te veranderen. Als we de reële en imaginaire termen groeperen, krijgen we:eix=(1−x22!+x44!−x66!+x88!−⋯)+i(x−x33!+x55!−x77!+⋯)Laten we nu even kijken naar de machtreeksen van sinus en cosinus. De machtreeks van cos⁡x is:cos⁡x=1−x22!+x44!−x66!+x88!−⋯En voor sin⁡x is het:sin⁡x=x−x33!+x55!−x77!+⋯Met andere woorden, de laatste vergelijking die we hadden is precies:eix=cos⁡x+isin⁡xwat de uitspraak van Euler’s formule is die we zochten.

Afleiding 2: Calculus

Een andere nette manier om Euler’s formule vast te stellen, is door zowel eix als cos⁡x+isin⁡x te beschouwen als functies van x, voordat we ze differentiëren om een gemeenschappelijke eigenschap over hen te vinden.

Daarvoor moeten we wel aannemen dat de functies ez, cos⁡x en sin⁡x gedefinieerd en differentieerbaar zijn voor alle reële getallen x en complexe getallen z. Door aan te nemen dat deze functies differentieerbaar zijn voor alle complexe getallen, is het ook mogelijk om aan te tonen dat Euler’s formule geldt voor alle complexe getallen.

Oké, luister eens even. Laten we f1(x) en f2(x) respectievelijk eix en cos⁡x+isin⁡x noemen. Als we f1 differentiëren met de kettingregel, krijgen we: f1′(x)=ieix=if1(x). En als we f2 differentiëren, krijgen we ook: f2′(x)=−sin⁡x+icos⁡x=if2(x). Beide functies voldoen dus aan de differentiaalvergelijking f′(x)=if(x). Nou, kijk eens naar de functie f1/f2. Die is goed gedefinieerd voor alle x (want f2(x)=cos⁡x+isin⁡x zijn punten op de eenheidscirkel, die nooit nul zijn). Als we de quotiëntregel hierop loslaten, krijgen we: (f1/f2)′(x)=(f1′(x)f2(x)−f1(x)f2′(x))/[f2(x)]2=(if1(x)f2(x)−f1(x)if2(x))/[f2(x)]2=0. Omdat de afgeleide nul is, moet f1/f2 een constante zijn. Welke waarde heeft die constante? Laten we x=0 invullen: (f1/f2)(0)=ei0/(cos⁡0+isin⁡0)=1. Dus voor alle x geldt: (f1/f2)(x)=eix/(cos⁡x+isin⁡x)=1. En dat is precies de formule die we zochten!

Afleiding 3: Poolcoördinaten

Joh, er is nog een superslimme manier om Euler’s formule te bewijzen. We gaan exponenten behandelen als getallen, of beter gezegd, als complexe getallen in poolcoördinaten.

Kijk, we weten al dat alle niet-nul complexe getallen op een unieke manier in poolcoördinaten kunnen worden uitgedrukt. Vooral getallen in de vorm eix (met x reëel) kunnen we schrijven als: eix=r(cos⁡θ+isin⁡θ). Hierbij is θ de hoofdhoek vanaf de positieve reële as (zeg maar 0≤θ<2π), en r is de straal (met r>0). We nemen niks aan over de waarden van r en θ, behalve dat ze functies van x zijn. We komen er vanzelf achter wat ze precies zijn.

(Maar hey, we weten wel dat als x=0, de linkerkant 1 is. Dat betekent dat r en θ moeten voldoen aan de beginvoorwaarden r(0)=1 en θ(0)=0.)

Oké, laten we beginnen met het differentiëren van beide kanten van de vergelijking. De linkerkant wordt ieix. Na het differentiëren van de rechterkant krijgen we: ieix=dr/dx(cos⁡θ+isin⁡θ)+r(−sin⁡θ+icos⁡θ)dθ/dx. We willen alles uitdrukken in r en θ. Om van eix af te komen, vervangen we het door r(cos⁡θ+isin⁡θ): ir(cos⁡θ+isin⁡θ)=(cos⁡θ+isin⁡θ)dr/dx+r(−sin⁡θ+icos⁡θ)dθ/dx. Als we de i links uitdelen, krijgen we: r(icos⁡θ−sin⁡θ)=(cos⁡θ+isin⁡θ)dr/dx+r(−sin⁡θ+icos⁡θ)dθ/dx. Als we de imaginaire en reële delengelijkstellen, krijgen we: ircos⁡θ=isin⁡θdr/dx+ircos⁡θdθ/dx en −rsin⁡θ=cos⁡θdr/dx−rsin⁡θdθ/dx. We hebben nu een systeem van twee vergelijkingen met twee onbekenden, waarbij dr/dx en dθ/dx de variabelen zijn. We lossen dit op in een paar stappen. Eerst noemen we dr/dx α en dθ/dx β: (I) rcos⁡θ=(sin⁡θ)α+(rcos⁡θ)β, (II) −rsin⁡θ=(cos⁡θ)α−(rsin⁡θ)β. Dan vermenigvuldigen we (I) met cos⁡θ en (II) met sin⁡θ: (III) rcos2⁡θ=(sin⁡θcos⁡θ)α+(rcos2⁡θ)β, (IV) −rsin2⁡θ=(sin⁡θcos⁡θ)α−(rsin2⁡θ)β. We doen dit om α weg te werken door (III) – (IV) te doen. Dan krijgen we: r(cos2⁡θ+sin2⁡θ)=r(cos2⁡θ+sin2⁡θ)β. Omdat cos2⁡θ+sin2⁡θ=1, wordt het simpeler: r=rβ. En omdat r>nooit nul is, betekent dit dat β – wat we hadden gezet als dθ/dx – gelijk is aan 1.

Als we dit resultaat terugzetten in (I) en (II) en wat dingen wegstrepen, krijgen we: 0=(sin⁡θ)α en 0=(cos⁡θ)α. Dat betekent dat α – wat we hadden gezet als dr/dx – gelijk moet zijn aan 0.

Omdat dr/dx=0, kunnen we concluderen dat r een constante moet zijn. En omdat dθ/dx=1, kunnen we concluderen dat θ=x+C voor een of andere constante C.

Maar omdat r voldoet aan de beginvoorwaarde r(0)=1, moet r=1 zijn. En omdat θ voldoet aan de beginvoorwaarde θ(0)=0, moet C=0 zijn. Dus θ=x.

Nu we r en θ hebben gevonden, kunnen we ze in de oorspronkelijke vergelijking zetten: eix=r(cos⁡θ+isin⁡θ)=cos⁡x+isin⁡x. En dat is precies Euler’s formule voor reële getallen x!

Toepassingen

Euler’s formule is een van de belangrijkste vergelijkingen in de wiskunde, dus je kunt er van op aan dat er een hoop interessante toepassingen zijn in verschillende onderwerpen. Bijvoorbeeld:

• De beroemde identiteit van Euler
• De exponentiële vorm van complexe getallen
• Alternatieve definities van goniometrische en hyperbolische functies
• Generalisatie van exponentiële en logaritmische functies naar complexe getallen
• Andere bewijzen van de stelling van de Moivre en trigonometrische optelformules

De identiteit van Euler

De identiteit van Euler wordt vaak beschouwd als de mooiste vergelijking in de wiskunde. Het wordt geschreven als

eiπ+1=0

waar het vijf van de belangrijkste constanten in de wiskunde laat zien. Dit zijn:

• De additieve identiteit 0
• De eenheid 1
• De Pi-constante π (verhouding van de omtrek van een cirkel tot zijn diameter)
• Het grondgetal van de natuurlijke logaritme e
• De imaginaire eenheid i

Hieronder zijn drie soorten getallen vertegenwoordigd: gehele getallen, irrationale getallen en imaginaire getallen. Ook drie van de basis wiskundige bewerkingen zijn vertegenwoordigd: optellen, vermenigvuldigen en machtsverheffen.

We krijgen Euler’s identiteit door te beginnen met Euler’s formule eix=cos⁡x+isin⁡x en door x=π te stellen en vervolgens de −1 naar de linkerkant te brengen. De tussenformule eiπ=−1 is gebruikelijk in de context van de trigonometrische eenheidscirkel in het complexe vlak: het komt overeen met het punt op de eenheidscirkel waarvan de hoek met de positieve reële as π is.

Complexe getallen in exponentiële vorm

Op dit punt weten we al dat een complex getal z kan worden uitgedrukt in Cartesiaanse coördinaten als x+iy, waarbij x en y respectievelijk het reële deel en het imaginaire deel van z zijn.

Inderdaad, hetzelfde complexe getal kan ook worden uitgedrukt in poolcoördinaten als r(cos⁡θ+isin⁡θ), waarbij r de grootte van de afstand tot de oorsprong is, en θ de hoek ten opzichte van de positieve reële as.

Maar daar houdt het niet op: dankzij de formule van Euler kan elk complex getal nu worden uitgedrukt als een complexe exponentiële als volgt:

z=r(cos⁡θ+isin⁡θ)=reiθ

waarbij r en θ dezelfde getallen zijn als hiervoor.

Om van (x,y) naar (r,θ) te gaan, gebruiken we de formules r=x2+y2 θ=atan2⁡(y,x) (waarbij atan2⁡(y,x) de tweevoudige arctangens functie is met atan2⁡(y,x)=arctan⁡(yx) wanneer x>0.)

Omgekeerd, om van (r,θ) naar (x,y) te gaan, gebruiken we de formules: x=rcos⁡θ y=rsin⁡θ De exponentiële vorm van complexe getallen maakt het ook veel makkelijker om complexe getallen te vermenigvuldigen – net zoals rechthoekige coördinaten optellen makkelijker maken. Bijvoorbeeld, gegeven twee complexe getallen z1=r1eiθ1 en z2=r2eiθ2, kunnen we ze nu als volgt vermenigvuldigen: z1z2=r1eiθ1⋅r2eiθ2=r1r2ei(θ1+θ2) In dezelfde geest kunnen we deze twee getallen ook delen als volgt: z1z2=r1eiθ1r2eiθ2=r1r2ei(θ1−θ2)

Als we in plaats daarvan de rechthoekige x+iy notatie hadden gebruikt, zou dezelfde deling vereist hebben dat we met de complex geconjugeerde in de teller en noemer vermenigvuldigen. Met de poolcoördinaten zou de situatie hetzelfde zijn geweest (misschien zelfs erger).

Als er iets is, maakt de exponentiële vorm het zeker makkelijker om te zien dat het vermenigvuldigen van twee complexe getallen eigenlijk hetzelfde is als het vermenigvuldigen van grootten en het optellen van hoeken, en dat het delen van twee complexe getallen eigenlijk hetzelfde is als het delen van grootten en het aftrekken van hoeken.

Alternatieve definities van sleutelfuncties

De formule van Euler kan ook worden gebruikt om alternatieve definities te geven voor sleutelfuncties zoals de complexe exponentiële functie, trigonometrische functies zoals sinus, cosinus en tangens, en hun hyperbolische tegenhangers. Het kan ook worden gebruikt om de relatie tussen sommige van deze functies vast te stellen.

Complexe exponentiële functie

Laten we beginnen met de herinnering dat de formule van Euler stelt dat eix=cos⁡x+isin⁡x Als we aannemen dat de formule alleen geldt voor reële x, dan is de exponentiële functie alleen gedefinieerd tot de imaginaire getallen. We kunnen de exponentiële functie echter ook uitbreiden om alle complexe getallen te omvatten – door een heel simpele truc te volgen:

ez=ex+iy(=exeiy)=dfex(cos⁡y+isin⁡y)

Met andere woorden, de exponentiële functie van het complexe getal x+iy is gewoon het complexe getal waarvan de grootte ex is en waarvan de hoek y is. Grappig genoeg betekent dit dat de complexe exponentiële functie verticale lijnen eigenlijk afbeeldt op cirkels. Hier is een animatie om het punt te illustreren:

Goniometrische functies

Naast het uitbreiden van het domein van de exponentiële functie, kunnen we de formule van Euler ook gebruiken om een vergelijkbare vergelijking af te leiden voor de tegenovergestelde hoek −x:e−ix=cos⁡x−isin⁡x Deze vergelijking, samen met de formule van Euler zelf, vormt een stelsel vergelijkingen waaruit we zowel de sinus- als de cosinusfunctie kunnen isoleren.

Als we bijvoorbeeld de e−ix-vergelijking aftrekken van de eix-vergelijking, vallen de cosinussen tegen elkaar weg en na delen door 2i krijgen we de complexe exponentiële vorm van de sinusfunctie:

sin⁡x=eix−e−ix2i

Op dezelfde manier, door de twee vergelijkingen bij elkaar op te tellen, vallen de sinussen tegen elkaar weg en na delen door 2 krijgen we de complexe exponentiële vorm van de cosinusfunctie:

cos⁡x=eix+e−ix2

Om het zeker te weten, hier is een video die dezelfde afleidingen in meer detail laat zien.

Aan de andere kant wordt de tangensfunctie gedefinieerd als sin⁡xcos⁡x, dus in termen van complexe exponentiële functies wordt het:

tan⁡x=eix−e−ixi(eix+e−ix)

Als bewezen is dat de formule van Euler geldt voor alle complexe getallen (zoals we deden in het bewijs via machtreeksen), dan zou hetzelfde gelden voor deze drie formules. Hun aanwezigheid stelt ons in staat om vrijelijk te schakelen tussen goniometrische functies en complexe exponentiële functies, wat een groot pluspunt is als het gaat om het berekenen van afgeleiden en integralen.

Hyperbolische functies

Naast goniometrische functies zijn hyperbolische functies nog een klasse van functies die kunnen worden gedefinieerd in termen van complexe exponentiële functies. Het is eigenlijk door deze connectie dat we een hyperbolische functie kunnen identificeren met zijn goniometrische tegenhanger.

Als we bijvoorbeeld beginnen met complexe sinus en complexe cosinus en iz invullen (en gebruik maken van de feiten dat i2=−1 en 1/i=−i), krijgen we:sin⁡iz=ei(iz)−e−i(iz)2i=e−z−ez2i=i(ez−e−z2)=isinh⁡zcos⁡iz=ei(iz)+e−i(iz)2=ez+e−z2=cosh⁡zHieruit kunnen we ook iz invullen in complexe tangens en krijgen:tan⁡(iz)=sin⁡izcos⁡iz=isinh⁡zcosh⁡z=itanh⁡zKortom, dit betekent dat we nu hyperbolische functies kunnen definiëren in termen van goniometrische functies als volgt:

sinh⁡z=sin⁡izicosh⁡z=cos⁡iztanh⁡z=tan⁡izi

Maar dit zijn niet de enige functies waaraan we nieuwe definities kunnen geven. In feite zijn de complexe logaritme en de algemene complexe exponentiële functie twee andere klassen van functies die we kunnen definiëren – als gevolg van de formule van Euler.

Complexe logaritme en algemene complexe exponentiële functie

De logaritme van een complex getal gedraagt zich op een bijzondere manier in vergelijking met de logaritme van een reëel getal. Meer specifiek heeft het een oneindig aantal waarden in plaats van één.

Om te zien hoe, beginnen we met de definitie van de logaritmische functie als de inverse van de exponentiële functie. Dat wil zeggen:eln⁡z=zln⁡(ez)=zVerder weten we ook dat voor elk paar complexe getallen z1 en z2 de optellingseigenschap voor exponenten geldt:ez1ez2=ez1+z2Dus, wanneer een niet-nul complex getal wordt uitgedrukt als een exponentiële functie, hebben we:z=|z|eiϕ=eln⁡|z|eiϕ=eln⁡|z|+iϕwaarbij |z| de grootte van z is en ϕ de hoek van z ten opzichte van de positieve reële as. En aangezien logaritme simpelweg de exponent is van een getal wanneer het tot de macht e wordt verheven, is de volgende definitie op zijn plaats:ln⁡z=ln⁡|z|+iϕOp het eerste gezicht lijkt dit een robuuste manier om de complexe logaritme te definiëren. Een tweede blik onthult echter dat de logaritme op deze manier gedefinieerd een oneindig aantal waarden kan aannemen – vanwege het feit dat ϕ ook kan worden gekozen als elk ander getal van de vorm ϕ+2πk (waarbij k een geheel getal is).

We hebben bijvoorbeeld eerder gezien dat e0=1 en e2πi=1. Dit betekent dat men de logaritme van 1 zou kunnen definiëren als zowel 0 als 2πi – of elk getal van de vorm 2πki (waarbij k een geheel getal is).

Om dit raadsel op te lossen, worden meestal twee aparte aanpakken gebruikt. De eerste aanpak is om de complexe logaritme simpelweg te beschouwen als een meerwaardige functie. Dat wil zeggen, een functie die elke input koppelt aan een set waarden. Één manier om dit te bereiken is door ln⁡z als volgt te definiëren:{ln⁡|z|+i(ϕ+2πk)}waar −π<ϕ≤π en k een geheel getal is. Hier zorgt de voorwaarde −π<ϕ≤π ervoor dat de hoek van z beperkt wordt tot slechts één kandidaat. Daarom wordt de ϕ die op deze manier gedefinieerd is meestal de hoofdhoek van z genoemd.

De tweede aanpak, die je zou kunnen zeggen eleganter is, is om de complexe logaritme van z simpelweg zo te definiëren dat ϕ de hoofdhoek van z is. Met dat begrip wordt de oorspronkelijke definitie dan welgedefinieerd:

ln⁡z=ln⁡|z|+iϕ

Bijvoorbeeld, onder deze nieuwe regel zouden we hebben dat ln⁡1=0 en ln⁡i=ln⁡(eiπ2)=iπ2. We zitten niet langer vast met het probleem van periodiciteit van hoeken!

Maar met de beperking dat −π<ϕ≤π, is het bereik van de complexe logaritme nu gereduceerd tot het rechthoekige gebied −π<y≤π (d.w.z. de hoofdtak). En als we de inverse relatie tussen logaritme en exponentieel willen behouden, moeten we hetzelfde doen voor het domein van de exponentiële functie.

Maar omdat de complexe logaritme nu welgedefinieerd is, kunnen we ook veel andere dingen erop baseren zonder in dubbelzinnigheid te belanden. Een voorbeeld daarvan zou de algemene complexe exponentieel (met een niet-nul basis a) zijn, die als volgt kan worden gedefinieerd:

az=eln⁡(az)=dfezln⁡a

Bijvoorbeeld, met behulp van de algemene complexe exponentieel zoals hierboven gedefinieerd, kunnen we nu een idee krijgen van wat ii eigenlijk betekent:ii=eiln⁡i=eiπ2i=e−π2≈0.208

Alternatieve bewijzen van de stelling van De Moivre en trigonometrische optelformules

De stelling die bekend staat als de stelling van De Moivre stelt dat

(cos⁡x+isin⁡x)n=cos⁡nx+isin⁡nx

waarbij x een reëel getal is en n een geheel getal. Standaard kan dit worden aangetoond door inductie (door het gebruik van enkele trigonometrische identiteiten), maar met behulp van de formule van Euler bestaat er nu een veel eenvoudiger bewijs.

Om te beginnen, herinner je dat de vermenigvuldigingseigenschap voor exponenten stelt dat(ez)k=ezkHoewel deze eigenschap over het algemeen niet waar is voor complexe getallen, geldt het wel in het speciale geval waar k een geheel getal is. Het is niet moeilijk om in te zien dat in dit geval de wiskunde in wezen neerkomt op herhaalde toepassingen van de optellingseigenschap voor exponenten.

En met dat geregeld, kunnen we de stelling van De Moivre gemakkelijk afleiden als volgt:(cos⁡x+isin⁡x)n=(eix)n=einx=cos⁡nx+isin⁡nxIn de praktijk wordt deze stelling vaak gebruikt om de wortels van een complex getal te vinden, en om gesloten uitdrukkingen voor sin⁡nx en cos⁡nx te verkrijgen. Het doet dit door functies die tot hoge machten zijn verheven te reduceren tot eenvoudige trigonometrische functies – zodat berekeningen gemakkelijk kunnen worden uitgevoerd.

De stelling van De Moivre is niet de enige stelling waarvan het bewijs kan worden vereenvoudigd als gevolg van de formule van Euler. Andere identiteiten, zoals de optelformules voor sin⁡(x+y) en cos⁡(x+y), profiteren ook van dat effect.

We weten inderdaad al dat voor alle reële x en y:cos⁡(x+y)+isin⁡(x+y)=ei(x+y)=eix⋅eiy=(cos⁡x+isin⁡x)(cos⁡y+isin⁡y)=(cos⁡xcos⁡y−sin⁡xsin⁡y)+i(sin⁡xcos⁡y+cos⁡xsin⁡y)Eenmaal daar, levert het gelijkstellen van de reële en imaginaire delen aan beide kanten de beroemde identiteiten op die we zochten:

cos⁡(x+y)=cos⁡xcos⁡y−sin⁡xsin⁡ysin⁡(x+y)=sin⁡xcos⁡y+cos⁡xsin⁡y

Conclusie

Zoals hierboven te zien is, is de formule van Euler een zeldzaam juweeltje in het rijk van de wiskunde. Het legt de fundamentele relatie tussen exponentiële en trigonometrische functies vast, en baant de weg voor veel ontwikkelingen in de wereld van complexe getallen, complexe functies en gerelateerde theorie.

Of het nu gaat om de identiteit van Euler of complexe logaritme, de formule van Euler lijkt geen steen onaangeroerd te laten wanneer uitdrukkingen zoals sin, i en e betrokken zijn. Het is een krachtig hulpmiddel waarvan de beheersing enorm lonend kan zijn, en om die reden is het een terechte kandidaat voor “de meest opmerkelijke formule in de wiskunde“.

Beschrijving	Verklaring
Formule van Euler	eix=cos⁡x+isin⁡x
Identiteit van Euler	eiπ+1=0
Complex getal (exponentiële vorm)	z=reiθ
Complexe exponentieel	ex+iy=ex(cos⁡y+isin⁡y)
Sinus (exponentiële vorm)	sin⁡x=eix−e−ix2i
Cosinus (exponentiële vorm)	cos⁡x=eix+e−ix2
Tangens (exponentiële vorm)	tan⁡x=eix−e−ixi(eix+e−ix)
Hyperbolische sinus (exponentiële vorm)	sinh⁡z=sin⁡izi
Hyperbolische cosinus (exponentiële vorm)	cosh⁡z=cos⁡iz
Hyperbolische tangens (exponentiële vorm)	tanh⁡z=tan⁡izi
Complexe logaritme	ln⁡z=ln⁡|z|+iϕ
Algemene complexe exponentieel	az=ezln⁡a
Stelling van De Moivre	(cos⁡x+isin⁡x)n=cos⁡nx+isin⁡nx
Additieve identiteit van sinus	sin⁡(x+y)=sin⁡xcos⁡y+cos⁡xsin⁡y
Additieve identiteit van cosinus	cos⁡(x+y)=cos⁡xcos⁡y−sin⁡xsin⁡y

Bronnen

• Wiskunde voor natuurkundigen (Susan M. Lea)
• Het Cambridge handboek van natuurkunde formules (Graham Woan)