À propos de la formule d’Euler

Dans le domaine des nombres complexes, lorsque nous intégrons des expressions trigonométriques, nous rencontrerons probablement la dénommée formule d’Euler.

Nommée d’après le mathématicien légendaire Leonhard Euler, cette puissante équation mérite un examen plus approfondi — afin que nous puissions l’utiliser à son plein potentiel.

Nous examinerons comment la formule d’Euler nous permet d’exprimer les nombres complexes sous forme d’exponentielles, et explorerons les différentes manières dont elle peut être établie avec une relative facilité.

De plus, nous considérerons également ses diverses applications telles que le cas particulier de l’identité d’Euler, la forme exponentielle des nombres complexes, les définitions alternatives des fonctions clés, et les preuves alternatives du théorème de De Moivre et des identités trigonométriques additives.

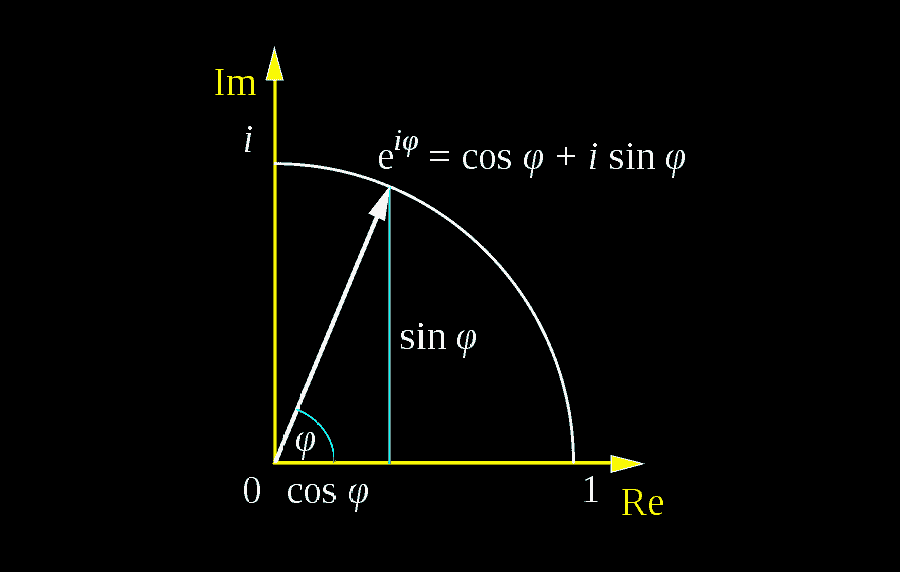
La formule d’Euler expliquée : Introduction, interprétation et exemples

Alors, qu’est-ce exactement que la formule d’Euler ? En résumé, il s’agit du théorème qui stipule que

eix=cos⁡x+isin⁡x

où :

• x est un nombre réel.
• e est la base du logarithme naturel.
• i est l’unité imaginaire (c’est-à-dire la racine carrée de −1).

La formule d’Euler établit la relation fondamentale entre les fonctions trigonométriques et les fonctions exponentielles. Géométriquement, elle peut être considérée comme un moyen de relier deux représentations du même nombre complexe unitaire dans le plan complexe.

Examinons quelques-unes des valeurs clés de la formule d’Euler, et voyons comment elles correspondent aux points du cercle trigonométrique/unitaire :

• Pour x=0, nous avons e0=cos⁡0+isin⁡0, ce qui donne 1=1. Jusqu’ici, tout va bien : nous savons qu’un angle de 0 sur le cercle trigonométrique est 1 sur l’axe réel, et c’est ce que nous obtenons ici.
• Pour x=1, nous avons ei=cos⁡1+isin⁡1. Ce résultat suggère que ei est précisément le point sur le cercle unitaire dont l’angle est 1 radian.
• Pour x=π2, nous avons eiπ2=cos⁡π2+isin⁡π2=i. Ce résultat est utile dans certains calculs liés à la physique.
• Pour x=π, nous avons eiπ=cos⁡π+isin⁡π, ce qui signifie que eiπ=−1. Ce résultat est équivalent à la célèbre identité d’Euler.
• Pour x=2π, nous avons ei(2π)=cos⁡2π+isin⁡2π, ce qui signifie que ei(2π)=1, comme pour x=0.

Une clé pour comprendre la formule d’Euler réside dans sa réécriture comme suit : (ei)x = cos x + i sin x où :

• L’expression de droite peut être considérée comme le nombre complexe unitaire avec un angle x.
• L’expression de gauche peut être considérée comme le nombre complexe unitaire d’un radian élevé à la puissance x.

Et puisque l’élévation d’un nombre complexe unitaire à une puissance peut être considérée comme des multiplications répétées (c’est-à-dire, l’addition d’angles dans ce cas), la formule d’Euler peut être interprétée comme deux manières différentes de parcourir le cercle unitaire pour arriver au même point.

Démonstrations

La formule d’Euler peut être établie d’au moins trois manières. La première démonstration est basée sur les séries entières, où les fonctions exponentielle, sinus et cosinus sont développées en séries entières pour conclure que la formule est effectivement valide.

La deuxième démonstration de la formule d’Euler est basée sur le calcul différentiel, dans lequel les deux côtés de l’équation sont traités comme des fonctions et différenciés en conséquence. Cela conduit ensuite à l’identification d’une propriété commune — qui peut être exploitée pour montrer que les deux fonctions sont effectivement égales.

Une autre démonstration de la formule d’Euler implique l’utilisation de coordonnées polaires dans le plan complexe, à travers lesquelles les valeurs de r et θ sont subséquemment trouvées. En fait, vous pourriez être en mesure de deviner ces valeurs — simplement en examinant la formule elle-même !

Démonstration 1 : Séries entières

L’une des démonstrations les plus intuitives de la formule d’Euler implique l’utilisation de séries entières. Elle consiste à développer les séries entières de l’exponentielle, du sinus et du cosinus — pour finalement conclure que l’égalité est vérifiée.

À titre de mise en garde, cette approche suppose que les développements en séries entières de sin z, cos z, et ez sont absolument convergents partout (c’est-à-dire qu’ils sont valables pour tous les nombres complexes z). Cependant, elle a également l’avantage de montrer que la formule d’Euler est valable pour tous les nombres complexes z.

Pour une variable complexe z, le développement en série entière de ez est ez = 1 + z/1! + z²/2! + z³/3! + z⁴/4! + ⋯ Maintenant, prenons z = ix (où x est un nombre complexe arbitraire). Lorsque z est élevé à des puissances croissantes, i est également élevé à des puissances croissantes. Les huit premières puissances de i se présentent ainsi : (par définition de i) i⁰ = 1 ; i⁴ = i² · i² = 1 ; i¹ = i ; i⁵ = i · i⁴ = i ; i² = −1 (par définition de i) ; i⁶ = i · i⁵ = −1 ; i³ = i · i² = −i ; i⁷ = i · i⁶ = −i (remarquez la cyclicité des puissances de i : 1, i, −1, −i. Nous utiliserons ces puissances sous peu.)

Avec z = ix, le développement de ez devient : eix = 1 + ix + (ix)²/2! + (ix)³/3! + (ix)⁴/4! + ⋯ En extrayant les puissances de i, nous obtenons : eix = 1 + ix − x²/2! − ix³/3! + x⁴/4! + ix⁵/5! − x⁶/6! − ix⁷/7! + x⁸/8! + ⋯ Et puisque le développement en série entière de ez est absolument convergent, nous pouvons réarranger ses termes sans en altérer la valeur. En regroupant les termes réels et imaginaires , nous obtenons : eix = (1 − x²/2! + x⁴/4! − x⁶/6! + x⁸/8! − ⋯) + i(x − x³/3! + x⁵/5! − x⁷/7! + ⋯) Maintenant, faisons un détour et examinons les séries entières du sinus et cosinus. La série entière de cos x est cos x = 1 − x²/2! + x⁴/4! − x⁶/6! + x⁸/8! − ⋯ Et pour sin x, c’est sin x = x − x³/3! + x⁵/5! − x⁷/7! + ⋯ En d’autres termes, la dernière équation que nous avions est précisément eix = cos x + i sin x, qui est l’énoncé de la formule d’Euler que nous recherchions.

Démonstration 2 : Calcul différentiel

Une autre manière élégante d’établir la formule d’Euler est de considérer à la fois eix et cos x + i sin x comme des fonctions de x, avant de les différencier pour trouver une propriété commune à leur sujet.

Pour que cela se produise, cependant, on doit supposer que les fonctions ez, cos x et sin x sont définies et différentiables pour tous les nombres réels x et les nombres complexes z. En supposant que ces fonctions sont différentiables pour tous les nombres complexes, il est également possible de montrer que la formule d’Euler est valable pour tous les nombres complexes.

Tout d’abord, soit f1(x) et f2(x) respectivement eix et cos⁡x+isin⁡x. En différenciant f1 via la règle de dérivation en chaîne, on obtient alors : f1′(x)=ieix=if1(x). De même, la différenciation de f2 donne également : f2′(x)=−sin⁡x+icos⁡x=if2(x). En d’autres termes, les deux fonctions satisfont l’équation différentielle f′(x)=if(x). Considérons maintenant la fonction f1/f2, qui est bien définie pour tout x (puisque f2(x)=cos⁡x+isin⁡x correspond à des points sur le cercle unitaire, qui ne sont jamais nuls). Cela étant établi, en utilisant la règle du quotient sur cette fonction, on obtient alors : (f1/f2)′(x)=f1′(x)f2(x)−f1(x)f2′(x)/[f2(x)]2=if1(x)f2(x)−f1(x)if2(x)/[f2(x)]2=0. Et puisque la dérivée ici est 0, cela implique que la fonction f1/f2 doit avoir été une constante dès le départ. Quelle est la valeur de cette constante ? Déterminons-la en substituant x=0 dans la fonction : (f1/f2)(0)=ei0/(cos⁡0+isin⁡0)=1. En d’autres termes, nous devons avoir pour tout x : (f1/f2)(x)=eix/(cos⁡x+isin⁡x)=1, ce qui, après avoir déplacé cos⁡x+isin⁡x à droite, devient la célèbre formule que nous recherchions.

Dérivation 3 : Coordonnées polaires

Une autre preuve ingénieuse de la formule d’Euler implique de traiter les exponentielles comme des nombres, ou plus précisément, comme des nombres complexes en coordonnées polaires.

En effet, nous savons déjà que tous les nombres complexes non nuls peuvent être exprimés de manière unique en coordonnées polaires. En particulier, tout nombre de la forme eix (avec x réel), qui est non nul, peut être exprimé comme : eix=r(cos⁡θ+isin⁡θ) où θ est son angle principal par rapport à l’axe réel positif (avec, disons, 0≤θ<2π), et r est son rayon (avec r>0). Nous ne faisons aucune hypothèse sur les valeurs de r et θ, excepté le fait qu’elles sont des fonctions de x (qui peuvent ou non contenir x comme variable). Elles seront déterminées au cours de la démonstration.

(Cependant, ce que nous savons, c’est que lorsque x=0, le côté gauche est 1, ce qui implique que r et θ satisfont les conditions initiales de r(0)=1 et θ(0)=0, respectivement.)

Pour ce que cela vaut, nous commencerons par différencier les deux côtés de l’équation. Par définition de l’exponentielle, différencier le côté gauche de l’équation par rapport à x donne ieix. Après avoir différencié le côté droit de l’équation, l’équation devient alors : ieix=dr/dx(cos⁡θ+isin⁡θ)+r(−sin⁡θ+icos⁡θ)dθ/dx. Nous recherchons une expression qui soit uniquement en termes de r et θ. Pour nous débarrasser de eix, nous substituons r(cos⁡θ+isin⁡θ) à eix pour obtenir : ir(cos⁡θ+isin⁡θ)=(cos⁡θ+isin⁡θ)dr/dx+r(−sin⁡θ+icos⁡θ)dθ/dx. Une fois là, en distribuant le i du côté gauche, on obtient : r(icos⁡θ−sin⁡θ)=(cos⁡θ+isin⁡θ)dr/dx+r(−sin⁡θ+icos⁡θ)dθ/dx. En égalant les parties imaginaires et parties réelles, respectivement, nous obtenons : ircos⁡θ=isin⁡θdr/dx+ircos⁡θdθ/dx et −rsin⁡θ=cos⁡θdr/dx−rsin⁡θdθ/dx. Ce que nous avons ici est un système de deux équations à deux inconnues, où dr/dx et dθ/dx sont les variables. Nous pouvons le résoudre en quelques étapes. Premièrement, en attribuant α à dr/dx et β à dθ/dx, nous obtenons : (I) (II) (I) rcos⁡θ=(sin⁡θ)α+(rcos⁡θ)β (II) −rsin⁡θ=(cos⁡θ)α−(rsin⁡θ)β. Deuxièmement, en multipliant (I) par cos⁡θ et (II) par sin⁡θ, nous obtenons : (III) (IV) (III) rcos2⁡θ=(sin⁡θcos⁡θ)α+(rcos2⁡θ)β (IV) −rsin2⁡θ=(sin⁡θcos⁡θ)α−(rsin2⁡θ)β. Le but de ces opérations est d’éliminer α en faisant (III) – (IV), et lorsque nous le faisons, nous obtenons : r(cos2⁡θ+sin2⁡θ)=r(cos2⁡θ+sin2⁡θ)β. Puisque cos2⁡θ+sin2⁡θ=1, une équation plus simple émerge : r=rβ. Et puisque r>≠0 pour tout x, cela implique que β — que nous avions défini comme étant dθ/dx — est égal à 1.

Une fois là, en substituant ce résultat dans (I) et (II) et en procédant à quelques annulations, nous obtenons : 0=(sin⁡θ)α 0=(cos⁡θ)α ce qui implique que α — que nous avons défini comme étant dr/dx — doit être égal à 0.

Du fait que dr/dx=0, nous pouvons déduire que r doit être une constante. De même, du fait que dθ/dx=1, nous pouvons déduire que θ=x+C pour une certaine constante C.

Cependant, puisque r satisfait la condition initiale r(0)=1, nous devons avoir r=1. De même, parce que θ satisfait la condition initiale θ(0)=0, nous devons avoir C=0. C’est-à-dire, θ=x.

Avec r et θ maintenant identifiés, nous pouvons alors les substituer dans l’équation originale et obtenir : eix=r(cos⁡θ+isin⁡θ)=cos⁡x+isin⁡x qui, comme prévu, est exactement l’énoncé de la formule d’Euler pour les nombres réels x.

Applications

Étant l’une des équations les plus importantes en mathématiques, la formule d’Euler a certainement sa part d’intéressantes applications dans différents domaines. Celles-ci incluent, entre autres :

• La célèbre identité d’Euler
• La forme exponentielle des nombres complexes
• Les définitions alternatives des fonctions trigonométriques et hyperboliques
• La généralisation des fonctions exponentielles et logarithmiques aux nombres complexes
• Démonstrations alternatives du théorème de de Moivre et des identités additives trigonométriques

L’identité d’Euler

L’identité d’Euler est souvent considérée comme l’équation la plus élégante en mathématiques. Elle s’écrit comme suit :

eiπ+1=0

où elle met en évidence cinq des constantes les plus importantes en mathématiques. Ces constantes sont :

• L’élément neutre de l’addition 0
• L’unité 1
• La constante Pi π (rapport entre la circonférence d’un cercle et son diamètre)
• La base du logarithme naturel e
• L’unité imaginaire i

Parmi ceux-ci, trois types de nombres sont représentés : les entiers, les nombres irrationnels et les nombres imaginaires. Trois des opérations mathématiques fondamentales sont également représentées : l’addition, la multiplication et l’exponentiation.

Nous obtenons l’identité d’Euler en partant de la formule d’Euler eix=cos⁡x+isin⁡x et en posant x=π, puis en transférant le −1 résultant dans le membre de gauche. La forme intermédiaire eiπ=−1 est courante dans le contexte du cercle trigonométrique unitaire dans le plan complexe : elle correspond au point sur le cercle unitaire dont l’angle par rapport à l’axe réel positif est π.

Nombres complexes sous forme exponentielle

À ce stade, nous savons déjà qu’un nombre complexe z peut être exprimé en coordonnées cartésiennes sous la forme x+iy, où x et y sont respectivement la partie réelle et la partie imaginaire de z.

En effet, le même nombre complexe peut également être exprimé en coordonnées polaires sous la forme r(cos⁡θ+isin⁡θ), où r est le module de sa distance à l’origine, et θ est son argument par rapport à l’axe réel positif.

Mais cela ne s’arrête pas là : grâce à la formule d’Euler, tout nombre complexe peut désormais être exprimé sous forme d’exponentielle complexe comme suit :

z=r(cos⁡θ+isin⁡θ)=reiθ

où r et θ sont les mêmes nombres qu’auparavant.

Pour passer de (x,y) à (r,θ), nous utilisons les formules r=x2+y2θ=atan2⁡(y,x) (où atan2⁡(y,x) est la fonction arctangente à deux arguments avec atan2⁡(y,x)=arctan⁡(yx) chaque fois que x0.)

Inversement, pour passer de (r,θ) à (x,y), nous utilisons les formules : x=rcos⁡θy=rsin⁡θ La forme exponentielle des nombres complexes facilite également la multiplication des nombres complexes — de la même manière que les coordonnées rectangulaires facilitent l’addition. Par exemple, étant donné deux nombres complexes z1=r1eiθ1 et z2=r2eiθ2, nous pouvons maintenant les multiplier comme suit : z1z2=r1eiθ1⋅r2eiθ2=r1r2ei(θ1+θ2) Dans le même esprit, nous pouvons également diviser les deux mêmes nombres comme suit : z1z2=r1eiθ1r2eiθ2=r1r2ei(θ1−θ2)

Si nous avions utilisé la notation rectangulaire x+iy à la place, la même division aurait nécessité la multiplication par le conjugué complexe au numérateur et au dénominateur. Avec les coordonnées polaires, la situation aurait été la même (voire peut-être pire).

Quoi qu’il en soit, la forme exponentielle permet de voir plus facilement que multiplier deux nombres complexes revient réellement à multiplier les modules et à additionner les arguments, et que diviser deux nombres complexes revient réellement à diviser les modules et à soustraire les arguments.

Définitions alternatives des fonctions clés

La formule d’Euler peut également être utilisée pour fournir des définitions alternatives aux fonctions clés telles que la fonction exponentielle complexe, les fonctions trigonométriques comme le sinus, le cosinus et la tangente, ainsi que leurs homologues hyperboliques. Elle peut également être utilisée pour établir la relation entre certaines de ces fonctions.

Fonction exponentielle complexe

Pour commencer, rappelons que la formule d’Euler stipule que eix=cos⁡x+isin⁡x Si la formule est supposée valide uniquement pour x réel, alors la fonction exponentielle n’est définie que jusqu’aux nombres imaginaires. Cependant, nous pouvons également étendre la fonction exponentielle pour inclure tous les nombres complexes — en suivant une astuce très simple :

ez=ex+iy(=exeiy)=dfex(cos⁡y+isin⁡y)

En d’autres termes, l’exponentielle du nombre complexe x+iy est simplement le nombre complexe dont le module est ex et dont l’argument est y. Il est intéressant de noter que cela signifie que l’exponentielle complexe fait essentiellement correspondre des lignes verticales à des cercles. Voici une animation pour illustrer ce point :

Fonctions trigonométriques

Outre l’extension du domaine de la fonction exponentielle, nous pouvons également utiliser la formule d’Euler pour dériver une équation similaire pour l’angle opposé −x : e−ix = cos x − i sin x. Cette équation, ainsi que la formule d’Euler elle-même, constituent un système d’équations à partir duquel nous pouvons isoler à la fois les fonctions sinus et cosinus.

Par exemple, en soustrayant l’équation e−ix de l’équation eix, les cosinus s’annulent et après division par 2i, nous obtenons la forme exponentielle complexe de la fonction sinus :

sin x = (eix − e−ix) / (2i)

De même, en additionnant les deux équations, les sinus s’annulent et après division par 2, nous obtenons la forme exponentielle complexe de la fonction cosinus :

cos x = (eix + e−ix) / 2

Pour s’en assurer, voici une vidéo illustrant les mêmes dérivations de manière plus détaillée.

D’autre part, la fonction tangente est définie comme étant sin x / cos x, donc en termes d’exponentielles complexes, elle devient :

tan x = (eix − e−ix) / (i(eix + e−ix))

Si la formule d’Euler est prouvée valable pour tous les nombres complexes (comme nous l’avons fait dans la démonstration par séries entières), alors il en serait de même pour ces trois formules. Leur présence nous permet de passer librement des fonctions trigonométriques aux exponentielles complexes, ce qui est un grand avantage lorsqu’il s’agit de calculer des dérivées et des intégrales.

Fonctions hyperboliques

En plus des fonctions trigonométriques, les fonctions hyperboliques constituent une autre classe de fonctions qui peuvent être définies en termes d’exponentielles complexes. En fait, c’est grâce à cette connexion que nous pouvons identifier une fonction hyperbolique à son homologue trigonométrique.

Par exemple, en partant du sinus complexe et du cosinus complexe et en y insérant iz (et en utilisant les faits que i2 = −1 et 1/i = −i), nous avons : sin iz = (ei(iz) − e−i(iz)) / (2i) = (e−z − ez) / (2i) = i(ez − e−z) / 2 = i sinh z; cos iz = (ei(iz) + e−i(iz)) / 2 = (ez + e−z) / 2 = cosh z. À partir de cela, nous pouvons également insérer iz dans la tangente complexe et obtenir : tan(iz) = sin iz / cos iz = i sinh z / cosh z = i tanh z. En bref, cela signifie que nous pouvons maintenant définir les fonctions hyperboliques en termes de fonctions trigonométriques comme suit :

sinh z = sin iz / i; cosh z = cos iz; tanh z = tan iz / i

Cependant, ce ne sont pas les seules fonctions auxquelles nous pouvons fournir de nouvelles définitions. En fait, le logarithme complexe et l’exponentielle complexe générale sont deux autres classes de fonctions que nous pouvons définir — résultant de la formule d’Euler.

Logarithme complexe et exponentielle complexe générale

Le logarithme d’un nombre complexe se comporte de manière particulière par rapport au logarithme d’un nombre réel. Plus précisément, il a un nombre infini de valeurs au lieu d’une seule.

Pour comprendre cela, nous commençons par la définition de la fonction logarithmique comme l’inverse de la fonction exponentielle. C’est-à-dire : eln z = z; ln(ez) = z. De plus, nous savons également que pour toute paire de nombres complexes z1 et z2, la propriété additive des exposants est valable : ez1ez2 = ez1+z2. Ainsi, lorsqu’un nombre complexe non nul est exprimé sous forme exponentielle, nous avons : z = |z|eiφ = eln |z|eiφ = eln |z|+iφ, où |z| est le module de z et φ est l’argument de z par rapport à l’axe réel positif. Et puisque le logarithme est simplement l’exposant d’un nombre lorsqu’il est élevé à e, la définition suivante s’impose : ln z = ln |z| + iφ. À première vue, cela semble être une manière robuste de définir le logarithme complexe. Cependant, un second regard révèle que le logarithme ainsi défini peut prendre un nombre infini de valeurs — en raison du fait que φ peut également être choisi comme n’importe quel autre nombre de la forme φ + 2πk (où k est un entier).

Par exemple, nous avons vu précédemment que e0 = 1 et e2πi = 1. Cela signifie que l’on pourrait définir le logarithme de 1 comme étant à la fois 0 et 2πi — ou n’importe quel nombre de la forme 2πki d’ailleurs (où k est un entier).

Pour résoudre ce dilemme, deux approches distinctes sont généralement employées. La première approche consiste simplement à considérer le logarithme complexe comme une fonction multivaluée. C’est-à-dire, une fonction qui associe à chaque entrée un ensemble de valeurs. Une manière d’y parvenir est de définir ln⁡z comme suit : {ln⁡|z|+i(ϕ+2πk)} où −π<ϕ≤π et k est un entier. Ici, la clause −π<ϕ≤π a pour effet de restreindre l’angle de z à un seul candidat. De ce fait, le ϕ ainsi défini est généralement appelé angle principal de z.

La seconde approche, qui est sans doute plus élégante, consiste simplement à définir le logarithme complexe de z de sorte que ϕ soit l’angle principal de z. Avec cette compréhension, la définition originale devient alors bien définie :

ln⁡z=ln⁡|z|+iϕ

Par exemple, selon cette nouvelle règle, nous aurions ln⁡1=0 et ln⁡i=ln⁡(eiπ2)=iπ2. Nous ne sommes plus confrontés au problème de la périodicité des angles !

Cependant, avec la restriction −π<ϕ≤π, le domaine du logarithme complexe est désormais réduit à la région rectangulaire −π<y≤π (c’est-à-dire la branche principale). Et si nous voulons préserver la relation inverse entre le logarithme et l’exponentielle, nous devrions également appliquer la même restriction au domaine de la fonction exponentielle.

Mais alors, puisque le logarithme complexe est maintenant bien défini, nous pouvons également définir de nombreuses autres choses basées sur celui-ci sans rencontrer d’ambiguïté. Un exemple serait l’exponentielle complexe générale (avec une base a non nulle), qui peut être définie comme suit :

az=eln⁡(az)=dfezln⁡a

Par exemple, en utilisant l’exponentielle complexe générale telle que définie ci-dessus, nous pouvons maintenant comprendre ce que signifie réellement ii : ii=eiln⁡i=eiπ2i=e−π2≈0,208

Preuves alternatives du théorème de De Moivre et des identités trigonométriques additives

Le théorème connu sous le nom de théorème de De Moivre énonce que

(cos⁡x+isin⁡x)n=cos⁡nx+isin⁡nx

où x est un nombre réel et n est un entier. Par défaut, cela peut être démontré par récurrence (en utilisant certaines identités trigonométriques), mais grâce à la formule d’Euler, une preuve beaucoup plus simple existe désormais.

Pour commencer, rappelons que la propriété multiplicative des exposants stipule que (ez)k=ezk Bien que cette propriété ne soit généralement pas vraie pour les nombres complexes, elle s’applique dans le cas particulier où k est un entier. En effet, il n’est pas difficile de voir que dans ce cas, les mathématiques se réduisent essentiellement à des applications répétées de la propriété additive des exposants.

Cela étant établi, nous pouvons alors facilement dériver le théorème de De Moivre comme suit : (cos⁡x+isin⁡x)n=(eix)n=einx=cos⁡nx+isin⁡nx En pratique, ce théorème est couramment utilisé pour trouver les racines d’un nombre complexe, et pour obtenir des expressions sous forme fermée pour sin⁡nx et cos⁡nx. Il le fait en réduisant des fonctions élevées à de hautes puissances à de simples fonctions trigonométriques — de sorte que les calculs puissent être effectués avec facilité.

En fait, le théorème de De Moivre n’est pas le seul théorème dont la preuve peut être simplifiée grâce à la formule d’Euler. D’autres identités, telles que les identités additives pour sin⁡(x+y) et cos⁡(x+y), bénéficient également de cet effet.

En effet, nous savons déjà que pour tous les réels x et y : cos⁡(x+y)+isin⁡(x+y)=ei(x+y)=eix⋅eiy=(cos⁡x+isin⁡x)(cos⁡y+isin⁡y)=(cos⁡xcos⁡y−sin⁡xsin⁡y)+i(sin⁡xcos⁡y+cos⁡xsin⁡y) Une fois là, en égalant les parties réelles et imaginaires des deux côtés, on obtient les fameuses identités que nous recherchions :

cos⁡(x+y)=cos⁡xcos⁡y−sin⁡xsin⁡y sin⁡(x+y)=sin⁡xcos⁡y+cos⁡xsin⁡y

Conclusion

Comme on peut le constater ci-dessus, la formule d’Euler est un joyau rare dans le domaine des mathématiques. Elle établit la relation fondamentale entre les fonctions exponentielles et trigonométriques, et ouvre la voie à de nombreux développements dans le monde des nombres complexes, des fonctions complexes et de la théorie associée.

En effet, qu’il s’agisse de l’identité d’Euler ou du logarithme complexe, la formule d’Euler semble ne laisser aucune pierre non retournée lorsque des expressions telles que sin, i et e sont impliquées. C’est un outil puissant dont la maîtrise peut être extrêmement gratifiante, et pour cette raison, elle est une candidate légitime au titre de “formule la plus remarquable des mathématiques“.

Formule d’Eulereix=cos⁡x+isin⁡x
Identité d’Eulereiπ+1=0
Nombre complexe (forme exponentielle)z=reiθ
Exponentielle complexeex+iy=ex(cos⁡y+isin⁡y)
Sinus (forme exponentielle)sin⁡x=eix−e−ix2i
Cosinus (forme exponentielle)cos⁡x=eix+e−ix2
Tangente (forme exponentielle)tan⁡x=eix−e−ixi(eix+e−ix)
Sinus hyperbolique (forme exponentielle)sinh⁡z=sin⁡izi
Cosinus hyperbolique (forme exponentielle)cosh⁡z=cos⁡iz
Tangente hyperbolique (forme exponentielle)tanh⁡z=tan⁡izi
Logarithme complexeln⁡z=ln⁡|z|+iϕ
Exponentielle complexe généraleaz=ezln⁡a
Théorème de De Moivre(cos⁡x+isin⁡x)n=cos⁡nx+isin⁡nx
Identité additive du sinussin⁡(x+y)=sin⁡xcos⁡y+cos⁡xsin⁡y
Identité additive du cosinuscos⁡(x+y)=cos⁡xcos⁡y−sin⁡xsin⁡y

Description	Énoncé

Sources

• Mathématiques pour physiciens (Susan M. Lea)
• Manuel de Cambridge des formules de physique (Graham Woan)