L’identité d’Euler est souvent considérée comme la formule la plus belle en mathématiques. Des individus la portent sur des T-shirts et se la font tatouer. Pourquoi donc ?
L’identité s’énonce comme suit
![[ e^{ipi }+1=0, ]](https://plus.maths.org/MI/17eab3c768113bf642698c4da7edf422/images/img-0001.png) |
 Leonhard Euler, 1707-1783. Portrait par Johann Georg Brucker.
Leonhard Euler, 1707-1783. Portrait par Johann Georg Brucker.
où 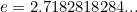 est la base du logarithme naturel,
est la base du logarithme naturel, 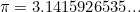 est le rapport entre la circonférence d’un cercle et son diamètre, et
est le rapport entre la circonférence d’un cercle et son diamètre, et 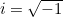 . Ces trois constantes sont d’une importance capitale en mathématiques — et puisque l’identité implique également
. Ces trois constantes sont d’une importance capitale en mathématiques — et puisque l’identité implique également  et
et  , nous obtenons une formule qui relie cinq des nombres les plus importants en mathématiques en utilisant quatre des opérations et relations mathématiques les plus fondamentales – l’addition, la multiplication, l’exponentiation et l’égalité. C’est pour cette raison que les mathématiciens affectionnent tant l’identité d’Euler.
, nous obtenons une formule qui relie cinq des nombres les plus importants en mathématiques en utilisant quatre des opérations et relations mathématiques les plus fondamentales – l’addition, la multiplication, l’exponentiation et l’égalité. C’est pour cette raison que les mathématiciens affectionnent tant l’identité d’Euler.
Mais d’où provient-elle et que signifie-t-elle ? Comme mentionné précédemment, 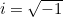 . Cela peut sembler surprenant car les nombres négatifs ne sont pas censés avoir de racines carrées. Cependant, si nous décrétons simplement que
. Cela peut sembler surprenant car les nombres négatifs ne sont pas censés avoir de racines carrées. Cependant, si nous décrétons simplement que 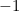 possède effectivement une racine carrée et que nous la nommons
possède effectivement une racine carrée et que nous la nommons 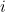 , nous pouvons alors construire une toute nouvelle classe de nombres, appelée les nombres complexes. Les nombres complexes ont la forme
, nous pouvons alors construire une toute nouvelle classe de nombres, appelée les nombres complexes. Les nombres complexes ont la forme 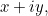 où
où  et
et 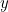 sont des nombres réels ordinaires (pour le nombre complexe
sont des nombres réels ordinaires (pour le nombre complexe 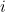 nous avons
nous avons 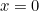 et
et 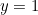 ). Veuillez consulter ici pour une introduction rapide aux nombres complexes et à leur calcul. Notez qu’un nombre réel peut également être considéré comme un nombre complexe. Le nombre
). Veuillez consulter ici pour une introduction rapide aux nombres complexes et à leur calcul. Notez qu’un nombre réel peut également être considéré comme un nombre complexe. Le nombre 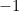 , par exemple, est un nombre complexe avec
, par exemple, est un nombre complexe avec 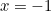 et
et 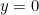 .
.
De la même manière qu’un nombre réel est représenté par un point sur une droite numérique, un nombre complexe  est représenté par un point dans le plan. Au nombre complexe
est représenté par un point dans le plan. Au nombre complexe 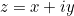 , nous associons le point de coordonnées
, nous associons le point de coordonnées 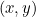 .
.
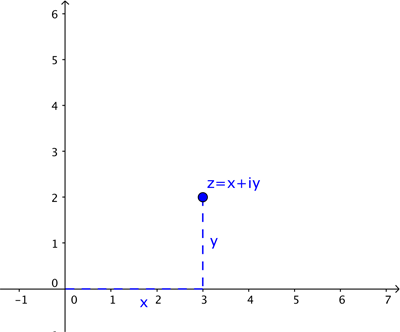
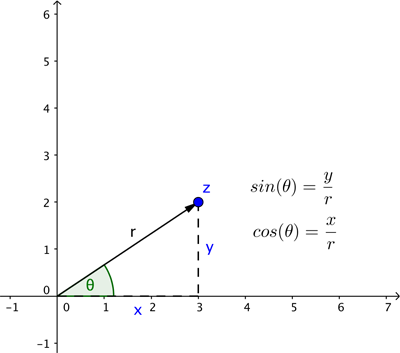
Dans cette description, nous avons utilisé les coordonnées cartésiennes : elles décrivent la position d’un point en indiquant la distance à parcourir dans la direction horizontale et la distance à parcourir dans la direction verticale. Cependant, il est parfois plus commode de décrire la position d’un point en termes de vecteur partant du point d’intersection des deux axes, comme illustré ci-dessous.
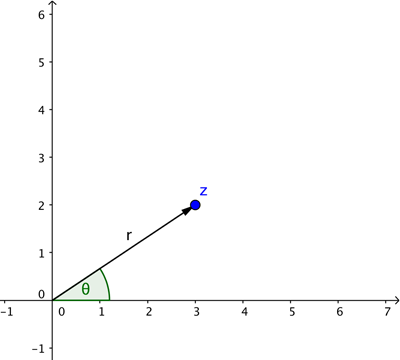
Pour définir ce vecteur, il est nécessaire de connaître sa longueur  et l’angle
et l’angle 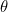 qu’il forme avec l’axe
qu’il forme avec l’axe  positif (mesuré dans le sens antihoraire). Ce sont les coordonnées polaires de notre point. La trigonométrie élémentaire (voir le diagramme ci-dessous) nous indique que si un point a pour coordonnées cartésiennes
positif (mesuré dans le sens antihoraire). Ce sont les coordonnées polaires de notre point. La trigonométrie élémentaire (voir le diagramme ci-dessous) nous indique que si un point a pour coordonnées cartésiennes 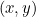 et pour coordonnées polaires
et pour coordonnées polaires 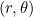 , alors
, alors
![[ x=r cos {( heta )} ]](https://plus.maths.org/MI/37f3a5d111741224a911781164a3c4b7/images/img-0006.png) |
et
![[ y=r sin {( heta )}. ]](https://plus.maths.org/MI/37f3a5d111741224a911781164a3c4b7/images/img-0007.png) |
Par conséquent, le nombre complexe  représenté par notre point,
représenté par notre point, 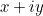 , peut également s’écrire
, peut également s’écrire
![[ z= r (cos {( heta )}+isin {( heta )}). ]](https://plus.maths.org/MI/c9570eacdeb0833cf294aca44d62bf7e/images/img-0003.png) |
Voici le point crucial. Il se trouve que pour les nombres réels  et
et 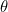
![[ r(cos {( heta )} + i sin {( heta )}) = re^{i heta }. ]](https://plus.maths.org/MI/c9570eacdeb0833cf294aca44d62bf7e/images/img-0006.png) |
Vous pouvez démontrer cela en utilisant les séries entières, consultez ici pour en savoir plus. C’est un fait remarquable que la fonction exponentielle et les deux fonctions trigonométriques sinus et cosinus soient liées de cette manière. Cela signifie que tout nombre complexe  peut s’écrire sous la forme
peut s’écrire sous la forme 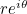 où
où  est la longueur de la ligne reliant le point du plan associé à
est la longueur de la ligne reliant le point du plan associé à  au point d’intersection des axes, et
au point d’intersection des axes, et 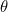 est l’angle que forme cette ligne avec l’axe
est l’angle que forme cette ligne avec l’axe  positif (mesuré dans le sens antihoraire).
positif (mesuré dans le sens antihoraire).
Ceci rend désormais l’identité d’Euler parfaitement limpide. Le nombre complexe 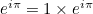 représente le point sur le plan à une distance
représente le point sur le plan à une distance  du point d’intersection des axes avec un angle associé de
du point d’intersection des axes avec un angle associé de 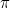 . Il s’agit du point aux coordonnées cartésiennes
. Il s’agit du point aux coordonnées cartésiennes 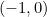 qui représente le nombre complexe
qui représente le nombre complexe 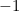 .
.
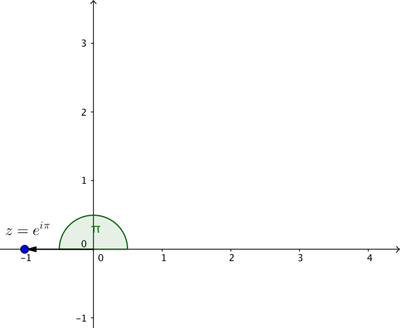
En réunissant tous ces éléments, nous constatons que
![[ e^{ipi } = -1, ]](https://plus.maths.org/MI/b7b172cee37d9c06da34d769912d2d57/images/img-0001.png) |
ce qui signifie que
![[ e^{ipi }+1 = 0. ]](https://plus.maths.org/MI/b7b172cee37d9c06da34d769912d2d57/images/img-0002.png) |
Et voilà l’identité d’Euler.












